An object of size 7.0 cm is placed at 27 cm in front of a concave mirror of focal length 18 cm. At what distance from the mirror should a screen be placed, so that a sharp focused image can be obtained? Find the size and the nature of the image.
Solution and Explanation
Object distance, \(u = −27\ cm\)
Object height, \(h = 7\ cm\)
Focal length, \(f = −18\ cm\)
According to the mirror formula,
\(\frac 1v+\frac 1u=\frac1f\)
\(\frac1v=\frac 1f-\frac 1u\)
\(\frac 1v=-\frac {1}{18}+\frac {1}{27}\)
\(\frac 1v=-\frac {1}{54}\)
\(v=-54\ cm\)
The screen should be placed at a distance of \(54\ cm\) in front of the given mirror.
Magnfication, \(m=-\frac {\text {Image\ distance}}{\text {Object\ distance}}\)
\(m =-\frac {54}{27}\)
\(m=-2\)
The negative value of magnification indicates that the image formed is real.
Magnfication, \(m=\frac {\text{Height\ of\ the\ image}}{\text {Height\ of\ the\ Object}}\)
\(m=\frac {h'}{h}\)
\(h'=m\times h\)
\(h'=7 \times (-2)\)
\(h'=-14\ cm\)
The negative value of image height indicates that the image formed is inverted.
Top Questions on Spherical Mirrors
- A concave mirror produces an image of an object such that the distance between the object and image is 20 cm. If the magnification of the image is \( -3 \), then the magnitude of the radius of curvature of the mirror is:
- JEE Main - 2025
- Physics
- Spherical Mirrors
- (ii) An object at a distance of 16 cm from a spherical mirror forms a virtual image at a distance of 12 cm behind the mirror. Determine the magnification of the image and type of the mirror.
- UP Board X - 2025
- Science
- Spherical Mirrors
- Image of an object formed by a concave mirror is real and of the size of the object. The object is placed -
- UP Board X - 2025
- Science
- Spherical Mirrors
- With the help of a suitable ray diagram, derive the formula \( \frac{1}{v} + \frac{1}{u} = \frac{1}{f} \) for a concave mirror.
- UP Board XII - 2025
- Physics
- Spherical Mirrors
- The length of the image formed by a concave mirror:
- UP Board XII - 2025
- Physics
- Spherical Mirrors
Questions Asked in CBSE X exam
Fermentation tanks are designed in the form of a cylinder mounted on a cone as shown below:

The total height of the tank is 3.3 m and the height of the conical part is 1.2 m. The diameter of the cylindrical as well as the conical part is 1 m. Find the capacity of the tank. If the level of liquid in the tank is 0.7 m from the top, find the surface area of the tank in contact with liquid.- CBSE Class X - 2025
- Mensuration
- The line \(2x - 3y = 6\) intersects x-axis at
- CBSE Class X - 2025
- Co-ordinate Geometry
- In the given graph, the polynomial \(p(x)\) is shown. Number of zeroes of \(p(x)\) is

- CBSE Class X - 2025
- Polynomials
- Comment on the significance of the title 'The Proposal' in the play. Provide two examples from the play to support your explanation.
- CBSE Class X - 2025
- The Proposal
Leaves of the sensitive plant move very quickly in response to ‘touch’. How is this stimulus of touch communicated and explain how the movement takes place?
- CBSE Class X - 2025
- Plant Biology
Concepts Used:
Spherical Mirrors
A spherical mirror is a mirror which has been cut out of a spherical surface.
There are two kinds of spherical mirrors:
- Convex Mirror
- Concave Mirror
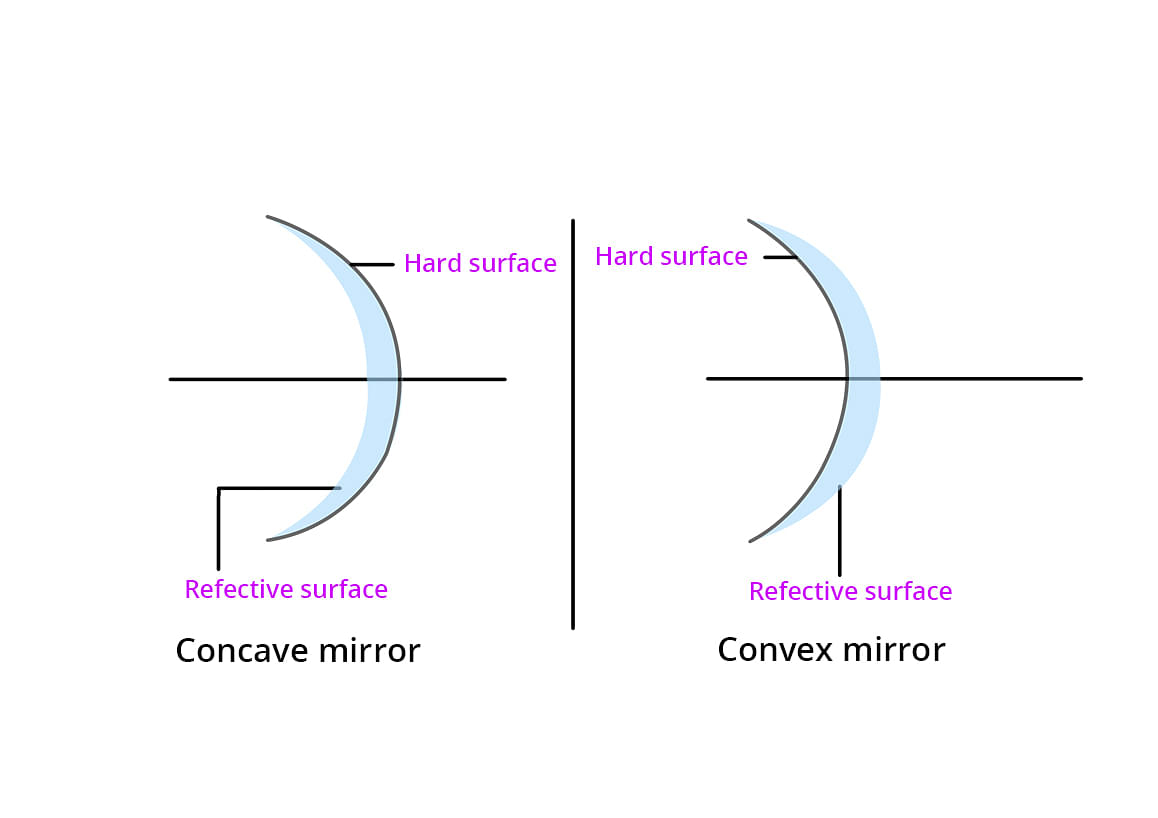
Concave Mirror
Concave mirrors are also called converging mirrors, because in these types of mirrors, light rays converge at a point after impact and reflect back from the reflective surface of the mirror.
Convex Mirror
The convex mirror has a reflective surface that is curved outward. Regardless of the distance between the subject and the mirrors, these mirrors are "always" virtual, upright and reduced.