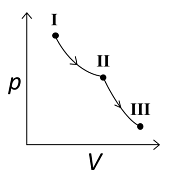
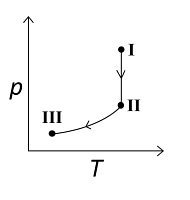
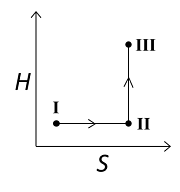
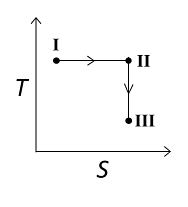
An ideal gas undergoes a reversible isothermal expansion from the state I to state II followed by a reversible adiabatic expansion from state II to state III. The correct plot(s) representing the changes from the state I to state III is(are)
(p: pressure, V: volume, T: temperature, H: enthalpy, S: entropy)
(p: pressure, V: volume, T: temperature, H: enthalpy, S: entropy)
The Correct Option is A, B, D
Solution and Explanation
For the reversible isothermal expansion from state I to II:
- Pressure decreases
- Volume increases
- Temperature remains constant
- Enthalpy (H) remains constant
- Entropy (S) increases
So, all options are correct for this expansion.
For the reversible adiabatic expansion from state II to III:
- Pressure decreases
- Volume increases
- Temperature decreases
- Enthalpy (H) decreases
- Entropy (S) remains constant
Option (C) does not follow the condition of decreasing enthalpy, so it is incorrect. Options (A), (B), and (D) all follow the conditions, so they are correct.
Therefore, correct graphical representations for the given conditions are (A), (B), and (D).
Top Questions on Enthalpy change
- Consider the following cases of standard enthalpy of reaction (\( \Delta H_f^\circ \) in kJ mol\(^{-1}\)): \[ \text{C}_2\text{H}_6(g) + 7 \text{O}_2(g) \rightarrow 2 \text{CO}_2(g) + 3 \text{H}_2\text{O}(l) \quad \Delta H_1^\circ = -1550 \] \[ \text{C(graphite)} + \text{O}_2(g) \rightarrow \text{CO}_2(g) \quad \Delta H_2^\circ = -393.5 \] \[ \text{H}_2(g) + \frac{1}{2} \text{O}_2(g) \rightarrow \text{H}_2\text{O}(g) \quad \Delta H_3^\circ = -286 \] The magnitude of \( \Delta H_f^\circ \) of \( \text{C}_2\text{H}_6(g) \) is \(\_\_\_\_\_\) kJ mol\(^{-1}\) (Nearest integer).
- JEE Main - 2025
- Chemistry
- Enthalpy change
- Given below are two statements:
Statement (I): The radius of isoelectronic species increases in the order: \[ \text{Mg}^{2+} < \text{Na}^{+} < \text{F}^{-} < \text{O}^{2-} \] Statement (II): The magnitude of electron gain enthalpy of halogens decreases in the order: \[ \text{Cl} > \text{F} > \text{Br} > \text{I} \] In light of the above statements, choose the most appropriate answer from the options given below:- JEE Main - 2025
- Chemistry
- Enthalpy change
- The incorrect relationship in the following pairs in relation to ionisation enthalpies is:
- JEE Main - 2025
- Chemistry
- Enthalpy change
- The group 14 elements A and B have the first ionisation enthalpy values of 708 and 715 kJ mol$^{-1}$ respectively. The above values are lowest among their group members. The nature of their ions A$^{2+}$ and B$^{4+}$ respectively is:
- JEE Main - 2025
- Chemistry
- Enthalpy change
- The bond dissociation energies of gaseous H2, Cl2, and HCl are 104, 58, and 103 kcal, respectively. The enthalpy of formation of HCl gas would be:
- BCECE - 2025
- Chemistry
- Enthalpy change
Questions Asked in JEE Advanced exam
Let $ a_0, a_1, ..., a_{23} $ be real numbers such that $$ \left(1 + \frac{2}{5}x \right)^{23} = \sum_{i=0}^{23} a_i x^i $$ for every real number $ x $. Let $ a_r $ be the largest among the numbers $ a_j $ for $ 0 \leq j \leq 23 $. Then the value of $ r $ is ________.
- JEE Advanced - 2025
- binomial expansion formula
- The total number of real solutions of the equation $$ \theta = \tan^{-1}(2 \tan \theta) - \frac{1}{2} \sin^{-1} \left( \frac{6 \tan \theta}{9 + \tan^2 \theta} \right) $$ is
(Here, the inverse trigonometric functions $ \sin^{-1} x $ and $ \tan^{-1} x $ assume values in $[-\frac{\pi}{2}, \frac{\pi}{2}]$ and $(-\frac{\pi}{2}, \frac{\pi}{2})$, respectively.)- JEE Advanced - 2025
- Inverse Trigonometric Functions
Let $ \mathbb{R} $ denote the set of all real numbers. Then the area of the region $$ \left\{ (x, y) \in \mathbb{R} \times \mathbb{R} : x > 0, y > \frac{1}{x},\ 5x - 4y - 1 > 0,\ 4x + 4y - 17 < 0 \right\} $$ is
- JEE Advanced - 2025
- Coordinate Geometry
The center of a disk of radius $ r $ and mass $ m $ is attached to a spring of spring constant $ k $, inside a ring of radius $ R>r $ as shown in the figure. The other end of the spring is attached on the periphery of the ring. Both the ring and the disk are in the same vertical plane. The disk can only roll along the inside periphery of the ring, without slipping. The spring can only be stretched or compressed along the periphery of the ring, following Hooke’s law. In equilibrium, the disk is at the bottom of the ring. Assuming small displacement of the disc, the time period of oscillation of center of mass of the disk is written as $ T = \frac{2\pi}{\omega} $. The correct expression for $ \omega $ is ( $ g $ is the acceleration due to gravity):

- JEE Advanced - 2025
- Waves and Oscillations
- Consider the vectors $$ \vec{x} = \hat{i} + 2\hat{j} + 3\hat{k},\quad \vec{y} = 2\hat{i} + 3\hat{j} + \hat{k},\quad \vec{z} = 3\hat{i} + \hat{j} + 2\hat{k}. $$ For two distinct positive real numbers $ \alpha $ and $ \beta $, define $$ \vec{X} = \alpha \vec{x} + \beta \vec{y} - \vec{z},\quad \vec{Y} = \alpha \vec{y} + \beta \vec{z} - \vec{x},\quad \vec{Z} = \alpha \vec{z} + \beta \vec{x} - \vec{y}. $$ If the vectors $ \vec{X}, \vec{Y}, \vec{Z} $ lie in a plane, then the value of $ \alpha + \beta - 3 $ is ________.
Concepts Used:
Enthalpy change
Enthalpy Change refers to the difference between the heat content of the initial and final state of the reaction. Change in enthalpy can prove to be of great importance to find whether the reaction is exothermic or endothermic.
Formula for change in enthalpy is:-
dH = dU + d(PV)
The above equation can be written in the terms of initial and final states of the system which is defined below:
UF – UI = qP –p(VF – VI)
Or qP = (UF + pVF) – (UI + pVI)
Enthalpy (H) can be written as H= U + PV. Putting the value in the above equation, we obtained:
qP = HF – HI = ∆H
Hence, change in enthalpy ∆H = qP, referred to as the heat consumed at a constant pressure by the system. At constant pressure, we can also write,
∆H = ∆U + p∆V
Standard Enthalpy of Reaction
To specify the standard enthalpy of any reaction, it is calculated when all the components participating in the reaction i.e., the reactants and the products are in their standard form. Therefore the standard enthalpy of reaction is the enthalpy change that occurs in a system when a matter is transformed by a chemical reaction under standard conditions.