Question

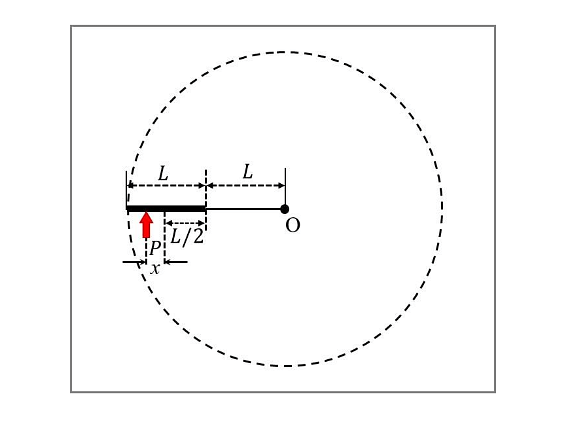
A thin uniform rod of length L and certain mass is kept on a frictionless horizontal table with a massless string of length L fixed to one end (top view is shown in the figure). The other end of the string is pivoted to a point O. If a horizontal impulse P is imparted to the rod at a distance x = L/n from the mid-point of the rod (see figure), then the rod and string revolve together around the point O, with the rod remaining aligned with the string. In such a case, the value of n is _____.

Answer 1

Step 1: Define Angular Impulse \( I_A \) 

\[ I_A = \text{angular impulse} = \vec{p} \times \vec{r} = \rho \left( \frac{l}{2} + x \right) \]

Step 2: Express Linear Impulse \( I \)

\[ I = \Delta p \]

Since \( p = mv - 0 \), we get:

\[ p = mv \]

Step 3: Write the Expression for \( I_A \)

\[ I_A = mv \times \left( \frac{3l}{2} + x \right) \]

Step 4: Define Angular Momentum \( L \)

\[ L = \text{angular momentum} = I_0 \omega + mv \times r \]

Substituting values:

\[ L = \frac{ml^2}{12} \omega + mv \times \frac{3l}{2} \]

Step 5: Relate Angular Impulse to Change in Angular Momentum

\[ mv \left( \frac{3l}{2} + x \right) = \frac{ml^2}{12} \omega + mv \frac{3l}{2} \]

Step 6: Solve for \( v \)

\[ mvx = \frac{ml^2}{12} \omega \]

Solving for \( v \):

\[ v = \frac{3l\omega}{2} \]

Step 7: Solve for \( x \)

\[ m\omega \cdot \frac{3l}{2} x = \frac{ml^2}{12} \times \omega \]

Solving for \( x \):

\[ x = \frac{l}{18} = \frac{l}{n} \]

Final Answer:

\( n = 18 \)