A thick current carrying cable of radius $'R'$ carries current $'I'$ uniformly distributed across its cross-section. The variation of magnetic field $B ( r )$ due to the cable with the distance $'r'$ from the axis of the cable is represented by :
The Correct Option is C
Solution and Explanation
Top Questions on Amperes circuital law
- A coil has a resistance of \( 30 \, \Omega \) and an inductive reactance of \( 20 \, \Omega \) at 50 Hz frequency. If an AC source of 200 V and 100 Hz is connected across the coil, then how much current will flow through the coil?
- MHT CET - 2024
- Physics
- Amperes circuital law
- In a series LCR circuit connected to an AC source, at resonance, the current is maximum because:
- MHT CET - 2024
- Physics
- Amperes circuital law
Consider the circuit shown :
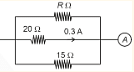The ammeter reads 0.9 A. Value of R is- JEE Main - 2024
- Physics
- Amperes circuital law
- Among the following, Ampere’s circuital law is represented by:
- AP EAPCET - 2023
- Physics
- Amperes circuital law
- In the given circuit, find the voltage drop VL in the load resistance RL
- WBJEE - 2023
- Physics
- Amperes circuital law
Questions Asked in NEET exam
- A container has two chambers of volumes \(V_1 = 2\) litres and \(V_2 = 3\) litres separated by a partition made of a thermal insulator. The chambers contain \(n_1 = 2\) moles and \(n_2 = 3\) moles of ideal gas at pressures \(p_1 = 1\) atm and \(p_2 = 2\) atm, respectively. When the partition is removed, the mixture attains an equilibrium pressure of :
- NEET (UG) - 2025
- Ideal Gases
A sphere of radius R is cut from a larger solid sphere of radius 2R as shown in the figure. The ratio of the moment of inertia of the smaller sphere to that of the rest part of the sphere about the Y-axis is :
- NEET (UG) - 2025
- Moment Of Inertia
The current passing through the battery in the given circuit, is:
- NEET (UG) - 2025
- Current electricity
A bob of heavy mass \(m\) is suspended by a light string of length \(l\). The bob is given a horizontal velocity \(v_0\) as shown in figure. If the string gets slack at some point P making an angle \( \theta \) from the horizontal, the ratio of the speed \(v\) of the bob at point P to its initial speed \(v_0\) is :
- NEET (UG) - 2025
- Pendulums
- Two cities X and Y are connected by a regular bus service with a bus leaving in either direction every T min. A girl is driving scooty with a speed of 60 km/h in the direction X to Y. She notices that a bus goes past her every 30 minutes in the direction of her motion, and every 10 minutes in the opposite direction. Choose the correct option for the period T of the bus service and the speed (assumed constant) of the buses.
- NEET (UG) - 2025
- Relative Velocity
Concepts Used:
Amperes circuital law
According to Ampere’s law, magnetic fields are related to the electric current that is produced in them. This law specifies that the magnetic field is associated with a given current or vice-versa, provided that the electric field doesn’t change with time.
Ampere’s circuital law can be written as the line integral of the magnetic field surrounding the closed loop which is equal to the number of times the algebraic sum of currents passing through the loop.
According to the second equation, if the magnetic field is integrated along the blue path, then it is equal to the current enclosed, I.
The magnetic field doesn’t vary at a distance r because of symmetry. The path length (in blue) in figure 1 has to be equal to the circumference of a circle,2πr.
