A modulating signal 2sin (6.28 × 106) t is added to the carrier signal 4sin(12.56 × 109) t for amplitude modulation. The combined signal is passed through a non-linear square law device. The output is then passed through a band pass filter. The bandwidth of the output signal of band pass filter will be ______MHz.
Correct Answer: 2
Solution and Explanation
WC=12.56×109
Wm=6.25×106
After amplitude modulation
Bandwidth frequency
=\(\frac{2W_m}{2_π}\)
=\(\frac{2×6.28}{2π}×10^6\)
=2 MHz
So, the answer is 2.
Top Questions on CHANGE OF STATE
- 1g of water, of volume 1 cm$^3$ at 100?C, is converted into steam at same temperature under normal atmospheric pressure ($\simeq$ ) $1\times 10^5$Pa . The volume of steam formed equals 1671 cm$^3$. If the specific latent heat of vaporisation of water is 2256 J/g, the change in internal energy is,
- NEET (UG) - 2019
- Physics
- CHANGE OF STATE
- Water standing in the open at $ {{32}^{o}}C $ evaporates because of the escape of some of the surface mole cuels. The heat of vaporisation (540 cal/g) is approximately equal to $ \varepsilon $ n, where $ \varepsilon $ is the average energy of the escaping molecules and n is the number of molecules per gram. The value of $ \varepsilon $ is close to
- AMUEEE - 2013
- Physics
- CHANGE OF STATE
- The latent heat of vaporisation of a substance is always
- AIIMS - 2010
- Physics
- CHANGE OF STATE
- One end of a copper rod of length 1.0 m and area of cross-section $ {{10}^{-3}}{{m}^{2}} $ is immersed in boiling water and the other end in ice. If the coefficient of thermal conductivity of copper is $ 92\text{ }cal\text{/}m-s\text{ }{}^\circ C $ and the latent heat of ice is $ 8\times {{10}^{4}}cal\text{/}kg, $ then the amount of ice which will melt in one minute is:
- JIPMER - 2002
- Physics
- CHANGE OF STATE
- Explain why :
- a body with large reflectivity is a poor emitter
- a brass tumbler feels much colder than a wooden tray on a chilly day
- an optical pyrometer (for measuring high temperatures) calibrated for an ideal black body radiation gives too low a value for the temperature of a red hot iron piece in the open, but gives a correct value for the temperature when the same piece is in the furnace
- the earth without its atmosphere would be inhospitably cold
- heating systems based on circulation of steam are more efficient in warming a building than those based on circulation of hot water
- CBSE Class XI
- Physics
- CHANGE OF STATE
Questions Asked in JEE Main exam
- A convex lens of focal length 40 cm forms an image of an extended source of light on a photo-electric cell. A current \( I \) is produced. The lens is replaced by another convex lens having the same diameter but focal length 20 cm. The photoelectric current now is:
- JEE Main - 2024
- Dual nature of matter
- For a sparingly soluble salt \( \text{AB}_2 \), the equilibrium concentrations of \( \text{A}^{2+} \) ions and \( \text{B}^- \) ions are \( 1.2 \times 10^{-4} \, \text{M} \) and \( 0.24 \times 10^{-3} \, \text{M} \), respectively. The solubility product of \( \text{AB}_2 \) is:
- JEE Main - 2024
- Method of Preparation of Diazoniun Salts
The portion of the line \( 4x + 5y = 20 \) in the first quadrant is trisected by the lines \( L_1 \) and \( L_2 \) passing through the origin. The tangent of an angle between the lines \( L_1 \) and \( L_2 \) is:
- JEE Main - 2024
- Tangents and Normals
- Let \[ \vec{a} = 2\hat{i} + \alpha \hat{j} + \hat{k}, \quad \vec{b} = -\hat{i} + \hat{k}, \quad \vec{c} = \beta \hat{j} - \hat{k}, \] where \( \alpha \) and \( \beta \) are integers and \( \alpha \beta = -6 \). Let the values of the ordered pair \( (\alpha, \beta) \) for which the area of the parallelogram of diagonals \( \vec{a} + \vec{b} \) and \( \vec{b} + \vec{c} \) is \( \frac{\sqrt{21}}{2} \), be \( (\alpha_1, \beta_1) \) and \( (\alpha_2, \beta_2) \). Then \( \alpha_1^2 + \beta_1^2 - \alpha_2 \beta_2 \) is equal to:
- JEE Main - 2024
- Vectors
- The molecular formula of second homologue in the homologous series of monocarboxylic acid is
- JEE Main - 2024
- Aldehydes, Ketones and Carboxylic Acids
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
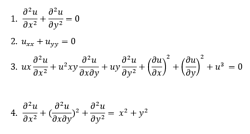
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
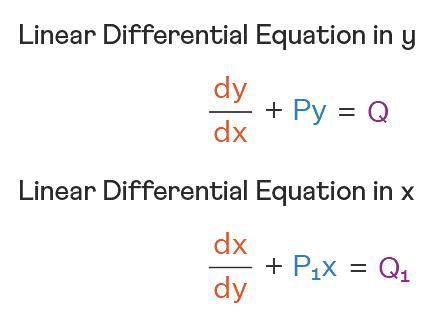
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations