Question:
A cube is subjected to a uniform volume compression. If the side of the cube decreases by $2\%$ the bulk strain is
A cube is subjected to a uniform volume compression. If the side of the cube decreases by $2\%$ the bulk strain is
Updated On: Dec 17, 2025
- 0.02
- 0.03
- 0.04
- 0.06
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
Given. $\frac{\Delta a}{a} \times 100=2$ where a is side length of cube.
Bulk strain $=\frac{\Delta V }{ V }$ Where
$V$ is volume ef cube for cube $V = a ^{3}$
differentiating both side w.r.t. V
$\frac{ dv }{ dv }=\frac{ da ^{3}}{ dv }=\frac{ d \left( a ^{3}\right)}{ da } \cdot \frac{ da }{ dv }$
$dv =3 a ^{2} \cdot da$
$\frac{ dv }{ v }=\frac{3 a ^{2} da }{ a ^{3}}=3 \cdot \frac{ da }{ a }$
$\frac{\Delta v }{ v }=3 x \frac{\Delta a }{ a }$
A putting values in this equationg
$\frac{\Delta V }{ V }=3 \times \frac{2}{100}=0.06$
Bulk strain $=\frac{\Delta V }{ V }$ Where
$V$ is volume ef cube for cube $V = a ^{3}$
differentiating both side w.r.t. V
$\frac{ dv }{ dv }=\frac{ da ^{3}}{ dv }=\frac{ d \left( a ^{3}\right)}{ da } \cdot \frac{ da }{ dv }$
$dv =3 a ^{2} \cdot da$
$\frac{ dv }{ v }=\frac{3 a ^{2} da }{ a ^{3}}=3 \cdot \frac{ da }{ a }$
$\frac{\Delta v }{ v }=3 x \frac{\Delta a }{ a }$
A putting values in this equationg
$\frac{\Delta V }{ V }=3 \times \frac{2}{100}=0.06$
Was this answer helpful?
1
0
Top Questions on elastic moduli
- The slope of the stress-strain curve in the elastic deformation region is
- JKCET - 2024
- Physics
- elastic moduli
- The law which states that within elastic limits strain produced is proportional to the stress producing it is known as
- JKCET - 2024
- Physics
- elastic moduli
- A wire of length L and radius r is clamped rigidly at one end. When the other end of the wire is pulled by a force F, its length increases by 5 cm. Another wire of the same material of length 4L and radius 4r is pulled by a force 4F under same conditions. The increase in length of this wire is ___ cm.
- JEE Main - 2022
- Physics
- elastic moduli
The elastic behavior of material for linear stress and linear strain, is shown in the figure. The energy density for a linear strain of 5×10–4 is ____ kJ/m3. Assume that material is elastic up to the linear strain of 5×10–4
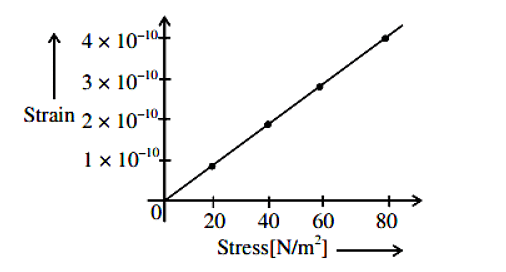
- JEE Main - 2022
- Physics
- elastic moduli
- If the length of a wire is made double and radius is halved of its respective values. Then, the Young’s modulus of the material of the wire will :
- JEE Main - 2022
- Physics
- elastic moduli
View More Questions
Questions Asked in BITSAT exam
- What is the dot product of the vectors \( \mathbf{a} = (2, 3, 1) \) and \( \mathbf{b} = (1, -1, 4) \)?
- BITSAT - 2025
- Vector Algebra
- Find the determinant of the matrix \( A = \begin{bmatrix} 2 & 3 \\ 4 & 5 \end{bmatrix} \).
- BITSAT - 2025
- Matrices
- A convex lens has focal length 20 cm. An object is placed at a distance of 40 cm from the lens. What is the position of the image formed?
- BITSAT - 2025
- Ray optics and optical instruments
- What is the value of \( \sin 30^\circ \)?
- BITSAT - 2025
- Trigonometry
- The area enclosed between the curve \(y = \log_e(x + e)\) and the coordinate axes is:
- BITSAT - 2025
- Fundamental Theorem of Calculus
View More Questions