Question:
A compound gives two fragments in a mass spectrometer. They are C19H7N+ and C19H50+. To separate peaks due to these fragments the instrument should have a resolution of
A compound gives two fragments in a mass spectrometer. They are C19H7N+ and C19H50+. To separate peaks due to these fragments the instrument should have a resolution of
Updated On: Jun 30, 2025
- They cannot be separated
- 2.417 x 10-2
- 3.402 × 104
- 1.042 × 104
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
The correct option is (D): 1.042 × 104
Was this answer helpful?
0
1
Top Questions on Mass spectrometry
- The major product in the given reaction sequence is Q. The mass spectrum of Q shows
([M] = molecular ion peak)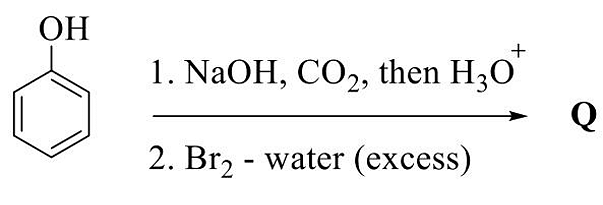
- GATE CY - 2024
- Inorganic Chemistry
- Mass spectrometry
- Which among the following characteristics of Laser light specifies the precise movement of all individual light waves together through time and space?
- AP PGECET - 2024
- Instrumentation Engineering
- Mass spectrometry
- Recombination of electron-hole produces ____ in LEDs.
- AP PGECET - 2024
- Instrumentation Engineering
- Mass spectrometry
- Magnetic sector analyzer is a part of
- AP PGECET - 2024
- Instrumentation Engineering
- Mass spectrometry
- Which ionization technique in mass spectrometry is most suitable for large biomolecules like proteins:
- GPAT - 2024
- Pharmaceutical Analysis
- Mass spectrometry
View More Questions
Questions Asked in GPAT exam
- Manufacturing Specification for tooling has been standardized by?
- GPAT - 2025
- Pharmacy Profession & Introduction to Pharmaceuticals
- If the label or the container bears the name of an individual or company purporting to be the manufacturer of the drug, which individual or company is fictitious or does not exist, it is:
- GPAT - 2025
- Drug therapy
- How much volume of Raw spirit can an excise officer withdraw as sample?
- GPAT - 2025
- Indian Pharmaceutical Industry- An Overview
- Match the following:
(1) Schedule FF
(2) Schedule F3
(3) Schedule V
(4) Schedule Y
Descriptions:
(P) Standards of patent and proprietary medicines
(Q) Requirements and guidelines for clinical trials
(R) Standards for sterilized umbilical tapes
(S) Standards for Ophthalmic preparations- GPAT - 2025
- Drug therapy
- Glycogenic amino acids enter TCA cycle except:
- GPAT - 2025
- Biochemistry
View More Questions