Question

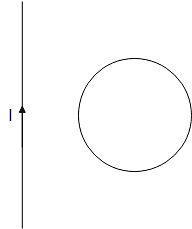
A circular coil is placed near a current-carrying conductor, both lying on the plane of the paper. The current is flowing through the conductor in such a way that the induced current in the loop is clockwise as shown in the figure. The current in the wire

 

• A. time-dependent and downward
• B. steady and upward
• C. time-dependent and upward
• D. An alternating current

Answer 1

The Correct Option is A

In this scenario, the loop is positioned to the right of the current-carrying wire, even though it might seem as if it's on the left side. This is because, when you move in the direction of the current, the loop is situated to the right.

Now, as the current diminishes, the induced current within the loop is in a clockwise direction (S), as illustrated in the diagram.

The correct option is (A): time-dependent and downward

Answer 2

To analyze the given problem, we need to use Faraday's Law of Induction and Lenz's Law. The setup involves a circular coil placed near a current-carrying conductor, both lying on the plane of the paper. The induced current in the loop is clockwise.
Analyzing the Induced Current
1. Understanding the Direction of the Induced Current:
  - The induced current in the loop is clockwise. According to Lenz's Law, the direction of the induced current is such that it opposes the change in magnetic flux that caused it.
2. Determining the Change in Magnetic Flux:
  - Since the induced current is clockwise, the magnetic flux through the loop must be increasing in the direction out of the plane of the paper (according to the right-hand rule). To oppose this change, the induced current creates a magnetic field into the plane of the paper.
3. Current in the Wire:
  - For the magnetic flux through the loop to be increasing out of the plane of the paper, the magnetic field created by the wire must be increasing and directed out of the plane of the paper at the location of the loop.
- Using the right-hand rule for the direction of the magnetic field around a current-carrying conductor, if the current is flowing downwards, the magnetic field on the side of the wire where the loop is located would be out of the plane of the paper.
4. Time-Dependence:
  - For the magnetic field (and thus the magnetic flux) to be increasing, the current in the wire must be increasing over time. This indicates that the current is not constant but time-dependent.
 Conclusion
Given that the induced current in the loop is clockwise, the current in the wire must be:
- Time-dependent (since the magnetic flux through the loop is changing).
- Flowing downwards (to create a magnetic field that is out of the plane of the paper at the loop's location).
Final Answer
The current in the wire is time-dependent and downward.