2NO + 2H2 → N2 + 2H2O
The above reaction has been studied at 800 °C. The related data is given in the table below.
The order of the reaction with respect to NO is ___.
The above reaction has been studied at 800 °C. The related data is given in the table below.
The order of the reaction with respect to NO is ___.
Correct Answer: 2
Approach Solution - 1
To determine the order of reaction with respect to NO, we analyze the provided reaction:
2NO + 2H2 → N2 + 2H2O
The rate equation for such reactions is generally expressed as:
Rate = k[NO]x[H2]y
where x and y are the reaction orders with respect to NO and H2, respectively. To find the reaction order with respect to NO (x), we need data from experiments showing how the reaction rate changes with concentration of NO.
| Experiment | [NO] (mol/L) | [H2] (mol/L) | Initial Rate (mol/L·s) |
|---|---|---|---|
| 1 | a | b | r1 |
| 2 | 2a | b | r2 |
Comparing experiments where only [NO] changes (experiment 1 and 2), we get:
(r2) / (r1) = ([2a]x[b]yk) / ([a]x[b]yk)
which simplifies to (r2) / (r1) = (2)x
If we assume r2 is directly 4 times r1, we have:
4 = 2x
Taking the logarithm base 2 of both sides, we get:
x = log2(4) = 2
Thus, the order of the reaction with respect to NO is 2.
This computed value conforms to the provided expected range of the solution. Therefore, the reaction order with respect to NO is confirmed to be 2.
Approach Solution -2
Let the rate of reaction (r) be given as:
\(r = K[\text{NO}]^n [\text{H}_2]^m\)
From the 1st data:
\( 0.135 = K[40]^n ... (65.6)^m ..... (1)\)
From the 2nd data:
\( 0.033 = K(20.1)^n \cdot (65.6)^m \quad \dots (2)\)
On dividing equation (1) by equation (2):
\[ \frac{0.135}{0.033} = \left( \frac{40}{20.1} \right)^n \]
\( 4 = (2)^n \)
Therefore, \( n = 2 \)
Hence, the order of reaction with respect to NO is 2.
Top Questions on Chemical Reactions of Alcohols Phenols and Ethers
- Phenol can be distinguished from propanol by using the reagent
- KCET - 2025
- Chemistry
- Chemical Reactions of Alcohols Phenols and Ethers
Calculate the potential for half-cell containing 0.01 M K\(_2\)Cr\(_2\)O\(_7\)(aq), 0.01 M Cr\(^{3+}\)(aq), and 1.0 x 10\(^{-4}\) M H\(^+\)(aq).
- CBSE CLASS XII - 2025
- Chemistry
- Chemical Reactions of Alcohols Phenols and Ethers
- Number of isomeric products formed by monochlorination Of \(2-methyl \) \(butane\) in presence of sunlight is
- JEE Main - 2024
- Chemistry
- Chemical Reactions of Alcohols Phenols and Ethers
- Find out the final product C

- JEE Main - 2024
- Chemistry
- Chemical Reactions of Alcohols Phenols and Ethers
- Moles of \(CH_4\) required for formation of \(22\) \(g\) of \(CO_2\) is \(m \times 10^{-2}\) The value of \(m\) is:
- JEE Main - 2024
- Chemistry
- Chemical Reactions of Alcohols Phenols and Ethers
Questions Asked in JEE Main exam
- The sum of all possible values of \( n \in \mathbb{N} \), so that the coefficients of \(x, x^2\) and \(x^3\) in the expansion of \((1+x^2)^2(1+x)^n\) are in arithmetic progression is :
- JEE Main - 2026
- Integration
- In a microscope of tube length $10\,\text{cm}$ two convex lenses are arranged with focal lengths $2\,\text{cm}$ and $5\,\text{cm}$. Total magnification obtained with this system for normal adjustment is $(5)^k$. The value of $k$ is ___.
- JEE Main - 2026
- Optical Instruments
Which one of the following graphs accurately represents the plot of partial pressure of CS₂ vs its mole fraction in a mixture of acetone and CS₂ at constant temperature?


- JEE Main - 2026
- Organic Chemistry
- Let \( ABC \) be an equilateral triangle with orthocenter at the origin and the side \( BC \) lying on the line \( x+2\sqrt{2}\,y=4 \). If the coordinates of the vertex \( A \) are \( (\alpha,\beta) \), then the greatest integer less than or equal to \( |\alpha+\sqrt{2}\beta| \) is:
- JEE Main - 2026
- Coordinate Geometry
- Three charges $+2q$, $+3q$ and $-4q$ are situated at $(0,-3a)$, $(2a,0)$ and $(-2a,0)$ respectively in the $x$-$y$ plane. The resultant dipole moment about origin is ___.
- JEE Main - 2026
- Electromagnetic waves
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
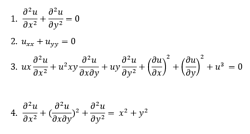
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
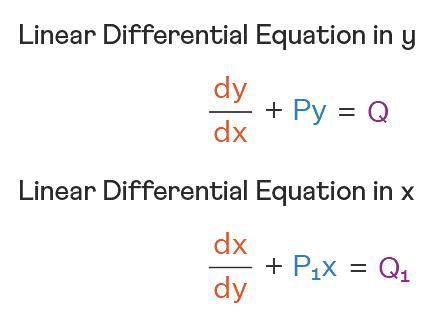
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations