Question

X-rays of wavelength λ get reflected from parallel planes of atoms in a crystal with spacing d between two planes as shown in the figure. If the two reflected beams interfare constructively,Then the condition for maxima will be(n is the order of interference fringe)

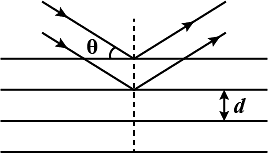
• A. d tanθ=nλ
• B. d sinθ=nλ
• C. 2d cosθ=nλ
• D. 2d sinθ=nλ

Answer 1

The Correct Option is D

Bragg’s Law and Path Difference Explanation: 

In X-ray diffraction by a crystal, waves are reflected from different parallel crystal planes. The key idea is that the path difference between the rays reflected from successive planes should lead to constructive interference.

Geometry Insight:

Let the distance between two successive crystal planes be d. An incident ray hits the first plane at an angle θ and reflects, while another ray enters to the second plane, reflects, and emerges parallel to the first ray.

The extra distance traveled by the second ray is the sum of two segments:

• AM = distance going into the plane = $d\sin\theta$
• AN = distance coming out of the plane = $d\sin\theta$

Total path difference = $AM + AN = 2d\sin\theta$

---

Condition for Constructive Interference:

To observe a strong reflected beam, the path difference should be an integer multiple of the wavelength λ, that is:

$2d\sin\theta = n\lambda$

Where:

• d = spacing between planes
• θ = glancing angle
• n = order of diffraction (an integer)
• λ = wavelength of X-ray

Conclusion: The correct relation that gives the condition for constructive interference in X-ray diffraction is:

Option (D): $2d\sin\theta = n\lambda$

Answer 2

Bragg's Law – Condition for Constructive Interference: 

When X-rays are incident on a crystal, they are reflected from different parallel planes of atoms within the crystal. Due to the regular spacing of these planes, interference occurs between the reflected waves.

Constructive interference (which leads to maxima or bright spots) happens when the extra path traveled by the wave reflected from the lower plane is an integer multiple of the wavelength.

Path difference between rays reflected from adjacent planes is:

\( \text{Path difference} = 2d\sin\theta \)

To satisfy the condition for constructive interference, this path difference must be equal to an integer multiple of the wavelength:

\( 2d\sin\theta = n\lambda \)

Where:

• \( d \) = distance between atomic planes in the crystal
• \( \theta \) = angle of incidence/reflection
• \( \lambda \) = wavelength of the X-rays
• \( n \) = order of the reflected beam (1st order, 2nd order, etc.)

Therefore, the correct option is: (D): \( 2d \sin \theta = n \lambda \)