Which one of the following has the same number of atoms as are in 6g of H2O
Which one of the following has the same number of atoms as are in 6g of H2O
0.4G He
22g CO2
1g H2
12g CO
The Correct Option is C
Solution and Explanation
To solve the problem, we need to find which option contains the same number of atoms as 6 g of H2O.
1. Calculate Moles of H2O:
Molar mass of water (H2O) = 18 g/mol
Moles of water = $ \frac{6}{18} = 0.333 \, \text{mol} $
2. Calculate Number of Atoms in H2O:
Each molecule of water contains 3 atoms (2 Hydrogen + 1 Oxygen).
So, total atoms = $0.333 \times 6.022 \times 10^{23} \times 3$
= $6.022 \times 10^{23} \times 1 = 6.022 \times 10^{23}$ atoms
3. Find Which Option Has the Same Number of Atoms:
- 1 g H2: Molar mass = 2 g/mol
Moles = $ \frac{1}{2} = 0.5 $ mol
Each H2 molecule has 2 atoms
Atoms = $0.5 \times 6.022 \times 10^{23} \times 2 = 6.022 \times 10^{23}$ - 0.4 g He: Molar mass = 4 g/mol → 0.1 mol → $0.1 \times 6.022 \times 10^{23}$ = fewer atoms
- 22 g CO2: Molar mass = 44 g/mol → 0.5 mol
Each CO2 has 3 atoms → $0.5 \times 3 \times 6.022 \times 10^{23}$ = $9.033 \times 10^{23}$ atoms - 12 g CO: Molar mass = 28 g/mol → $ \frac{12}{28} \approx 0.43 $ mol
Each CO has 2 atoms → $0.43 \times 2 \times 6.022 \times 10^{23} \approx 5.2 \times 10^{23}$ atoms
Final Answer:
The option with the same number of atoms as in 6 g of water is 1 g H2.
Top Questions on Law Of Chemical Equilibrium And Equilibrium Constant
- Consider the equilibrium: \[ \text{CO(g)} + \text{3H}_2\text{(g)} \rightleftharpoons \text{CH}_4\text{(g)} + \text{H}_2\text{O(g)} \] If the pressure applied over the system increases by two fold at constant temperature then:
- JEE Main - 2025
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
The equilibrium constant for decomposition of $ H_2O $ (g) $ H_2O(g) \rightleftharpoons H_2(g) + \frac{1}{2} O_2(g) \quad (\Delta G^\circ = 92.34 \, \text{kJ mol}^{-1}) $ is $ 8.0 \times 10^{-3} $ at 2300 K and total pressure at equilibrium is 1 bar. Under this condition, the degree of dissociation ($ \alpha $) of water is _____ $\times 10^{-2}$ (nearest integer value). [Assume $ \alpha $ is negligible with respect to 1]
- JEE Main - 2025
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- In the following system, $ PCl_5(g) \rightleftharpoons PCl_3(g) + Cl_2(g) $ at equilibrium, upon addition of xenon gas at constant T and p, the concentration of
- JEE Main - 2025
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- Given below are two statements:
Statement I: A catalyst cannot alter the equilibrium constant ($ K_c $) of the reaction, temperature remaining constant.
Statement II: A homogeneous catalyst can change the equilibrium composition of a system, temperature remaining constant.
In the light of the above statements, choose the correct answer from the options given below.- JEE Main - 2025
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
- What is the pH of 0.365% (w/V) HCl aqueous solution? (HCl=36.5 u), (log 0.365=−0.4377)
- TS EAMCET - 2025
- Chemistry
- Law Of Chemical Equilibrium And Equilibrium Constant
Questions Asked in TS EAMCET exam
- Match the following and choose the correct option from the lists given below:

- TS EAMCET - 2025
- Microbiology
- $7\hat{i}-4\hat{j}+7\hat{k}, \hat{i}-6\hat{j}+10\hat{k}, -\hat{i}-3\hat{j}+4\hat{k}, 5\hat{i}-\hat{j}+\hat{k}$ are the position vectors of the points A, B, C, D respectively. If $p\hat{i} + q\hat{j} + r\hat{k}$ is the position vector of the point of intersection of the diagonals of the quadrilateral ABCD, then $p+q+r=$
- TS EAMCET - 2025
- Vector Algebra
- If the sum of two vectors is a unit vector, then the magnitude of their difference is:
- A particle is executing simple harmonic motion with an amplitude of 10 cm. If the kinetic energy of the particle at a distance of 6 cm from the mean position is 100 J, then the kinetic energy of the particle at a distance of 2 cm from the mean position is
- TS EAMCET - 2025
- Waves and Oscillations
- Which of the following is an example of antifertility drug?
- TS EAMCET - 2025
- Chemistry in Everyday Life
Concepts Used:
Law of Chemical Equilibrium
Law of Chemical Equilibrium states that at a constant temperature, the rate of a chemical reaction is directly proportional to the product of the molar concentrations of the reactants each raised to a power equal to the corresponding stoichiometric coefficients as represented by the balanced chemical equation.
Let us consider a general reversible reaction;
A+B ↔ C+D
After some time, there is a reduction in reactants A and B and an accumulation of the products C and D. As a result, the rate of the forward reaction decreases and that of backward reaction increases.
Eventually, the two reactions occur at the same rate and a state of equilibrium is attained.
By applying the Law of Mass Action;
The rate of forward reaction;
Rf = Kf [A]a [B]b
The rate of backward reaction;
Rb = Kb [C]c [D]d
Where,
[A], [B], [C] and [D] are the concentrations of A, B, C and D at equilibrium respectively.
a, b, c, and d are the stoichiometric coefficients of A, B, C and D respectively.
Kf and Kb are the rate constants of forward and backward reactions.
However, at equilibrium,
Rate of forward reaction = Rate of backward reaction.
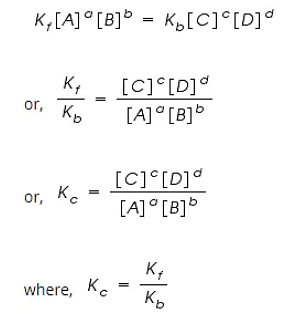
Kc is called the equilibrium constant expressed in terms of molar concentrations.
The above equation is known as the equation of Law of Chemical Equilibrium.