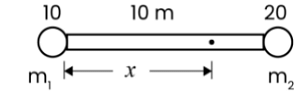
Two objects of mass 10 kg and 20 kg respectively are connected to the two ends of a rigid rod of length 10 m with negligible mass. The distance of the center of mass of the system from the 10 kg mass is:
- \(\frac{10}{3} m\)
- \(\frac{20}{3} m\)
- \(10 m\)
- \(5 m\)
The Correct Option is B
Solution and Explanation
The correct option is (B) : \(\frac{20}{3} m\).
\(x = [\frac{m_{2r}}{(m_1+m_2)}]\)
\(= [\frac{20(20)}{(20+10)}]\)
\(= \frac{200}{30}\)
\(= \frac{20}{3}\)
Top Questions on momentum
- A body of mass 10 kg is moving with a speed of 5 m/s. What is the momentum of the body?
- An object of mass \( m \) is projected from the origin in a vertical \( xy \)-plane at an angle \( 45^\circ \) with the x-axis with an initial velocity \( v_0 \). The magnitude and direction of the angular momentum of the object with respect to the origin, when it reaches the maximum height, will be:
Given below are two statements. One is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A): Knowing the initial position \( x_0 \) and initial momentum \( p_0 \) is enough to determine the position and momentum at any time \( t \) for a simple harmonic motion with a given angular frequency \( \omega \).
Reason (R): The amplitude and phase can be expressed in terms of \( x_0 \) and \( p_0 \).
In the light of the above statements, choose the correct answer from the options given below:- A particle moves under the influence of a force in the XY-plane such that the components of its linear momentum $\vec{p}$ at any time $t$ are given by $p_x = p \sin t$ and $p_y = p \cos t$. The angle between $\vec{F}$ and $\vec{p}$ at that time is
- KEAM - 2024
- Physics
- momentum
Which of the following graph shows the variation of velocity with mass for the constant momentum?
Questions Asked in NEET exam
- In an ideal transformer, the turns ratio is \(N_p/N_s\) =1/2 .The ratio \(V_S:V_P\) is equal to (the symbols carry their usual meaning):
- NEET (UG) - 2024
- Transformers
- Match List I with List II:Choose the correct answer from the options given below:
List I
List II
A Mesozoic Era I Lower invertebrates B Proterozoic Era II Fish & Amphibia C Cenozoic Era III Birds & Reptiles D Paleozoic Era IV Mammals - NEET (UG) - 2024
- Origin Of Life
- In a plant, black seed color (BB/Bb) is dominant over white seed color (bb). In order to find out the genotype of the black seed plant, with which of the following genotype will you cross it?
- NEET (UG) - 2024
- monohybrid cross
- The correct IUPAC name of the compound
- NEET (UG) - 2024
- Nomenclature Of Organic Compounds
- A sheet is placed on a horizontal surface in front of a strong magnetic pole. A force is needed to :
A. hold the sheet there if it is magnetic.
B. hold the sheet there if it is non-magnetic.
C. move the sheet away from the pole with uniform velocity if it is conducting.
D. move the sheet away from the pole with uniform velocity if it is both, non-conducting and non-polar.
Choose the correct statement(s) from the options given below :- NEET (UG) - 2024
- Magnetic Field
Concepts Used:
Momentum
It can be defined as "mass in motion." All objects have mass; so if an object is moving, then it is called as momentum.
the momentum of an object is the product of mass of the object and the velocity of the object.
Momentum = mass • velocity
The above equation can be rewritten as
p = m • v
where m is the mass and v is the velocity.
Momentum is a vector quantity and the direction of the of the vector is the same as the direction that an object.