Question

The uncertainty in momentum of an electron is $1\times 10^{-5} kg m/s.$ The uncertainty in its position will be (Given, $h = 6.62 \times 10^{-34} kg m^2/s)$

• A. $1.05 \times 10^{-28} m$
• B. $1.05 \times 10^{-26} m$
• C. $5.27 \times 10^{-30} m$
• D. $5.25 \times 10^{-28} m$

Answer 1

The Correct Option is C

The uncertainty in the momentum of an electron is 1 × 10^-5 kgm/s

According to the uncertainty principle, it is impossible to precisely identify a particle's position and momentum at the same time. Position and momentum always produce a result that is greater than h/4. The Heisenberg Uncertainty Principle's formula is as:
\(\Delta p \times \Delta x \ge\frac{h}{4\pi}\) 

Here, h is the Planck’s constant ( 6.62607004 × 10^-34 m² kg / s)

Δp is the uncertainty in momentum

Δx is the uncertainty in position

So, Δp = 1 × 10^-5 kgm/s
So, the Uncertainty in position(Δx)  will be- 
\(\hspace15mm \Delta p=1\times10^{-5} kg m/s\)
\(1\times10^{-5}\times \Delta x=\frac{6.62 \times 10^{-34}}{4\times\frac{22}{7}}\)
\(\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \Delta x=\frac{6.62 \times 10^{-34}\times 7}{10^{-5}\times 4\times 22}\)
\(= 5.265 \times 10^{-30} m\)
\(\approx 5.27 \times 10^{-30} m\)

Uncertainty is a basic characteristic of nature. 

• We, therefore, came to the conclusion that it is challenging to precisely and concurrently identify a particle's location and momentum. 
• Therefore, the concepts of precise location and precise velocity are useless. 
• This concept won't be revealed by ordinary scientific experience. It is because it is easy to determine an object's velocity and position. 
• This is due to the fact that the implied uncertainty of this concept for typical things is too modest to be seen. 
• Because of this, the uncertainty in location and velocity is more than or equal to h, a very, very tiny physical quantity. 
• Because of this, this product of uncertainty will only have a very minor impact on atoms and subatomic particles.

Discover more from this chapter: Structure of Atom

Answer 2

The Correct Answer is (C)

Real Life Applications

• The design of electron microscopes certainly uses uncertainty principle .
• The uncertainty principle limits how accurately the position of an electron can be determined, which limits the resolution of an electron microscope.

• In order to improve the resolution of an electron microscope, the uncertainty in the momentum of the electron instructed to be reduced.

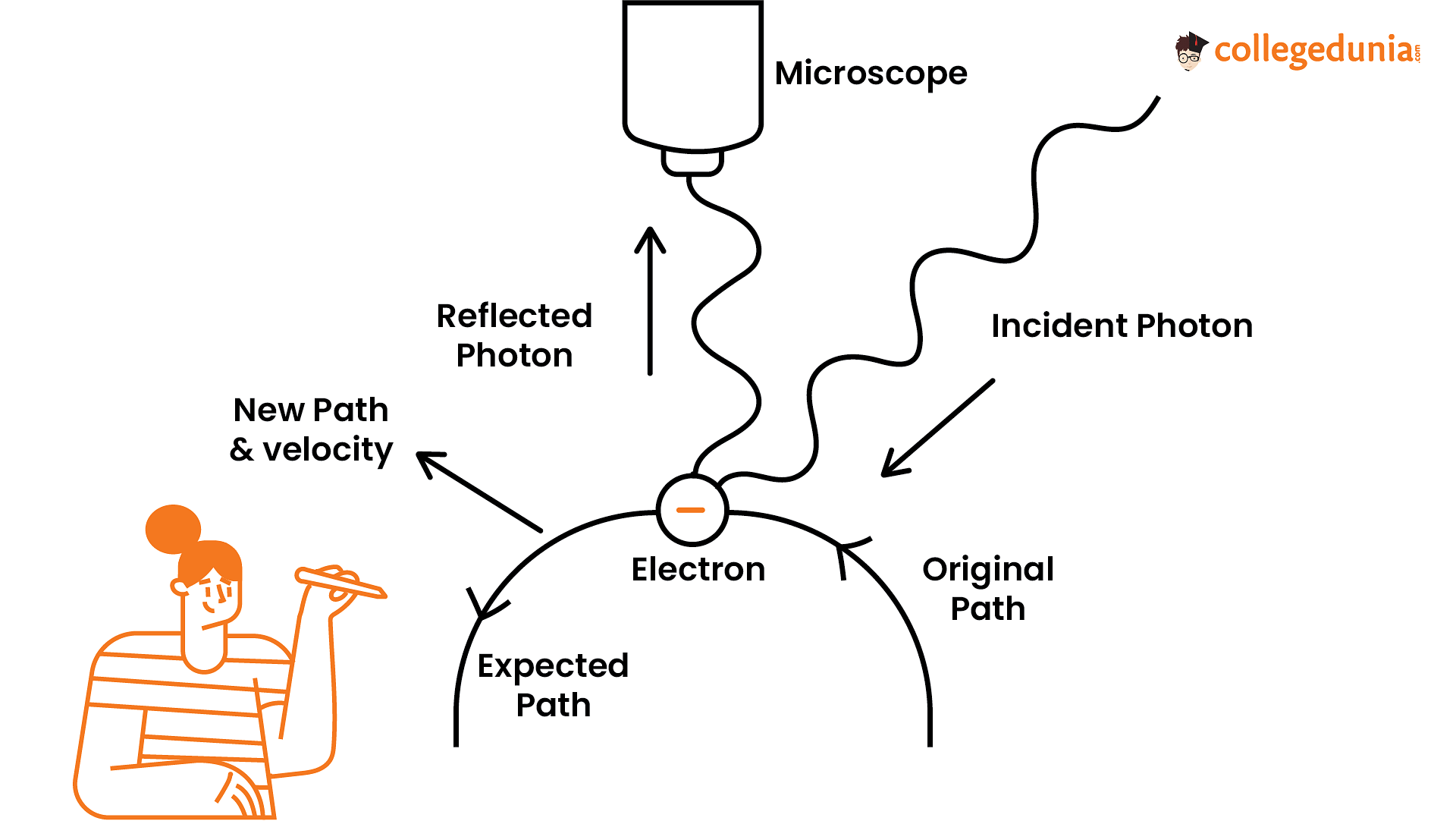
Question can also be asked as

• What is the uncertainty in the position of an electron if the uncertainty in its momentum is 1× 10-5 kg m/s?
• How does the uncertainty principle relate the uncertainty in the position and momentum of an electron?
• What is the minimum uncertainty in the position of an electron, given the uncertainty in its momentum?

Answer 3

In this theory, x is regarded as an error in the measurement of location, whereas p is regarded as a mistake in the measurement of momentum. As a result of this idea, we can write:

Δ X × Δ p ≥ \(\frac{h}{4\pi}\)

Momentum p = mv can also be written as

Δ X × Δ mv ≥ \(\frac{h}{4\pi}\)

A more significant inaccuracy in the measurement of the other variable is automatically revealed by an accurate measurement of position or momentum.

Now, apply Heisenberg’s Principle to an electron in an orbit of an atom, with h = 6.626 ×

where h = 6.626 × 10^-34 Js and m= 9.11 ×10^-31Kg,

∆x × ∆v ≥ \(\frac {6.626 × 10^{-34}}{4×3.14×9.11×10^{-31}}\)

= 10^-4 m² s^-1.

Only microscopic particles with dual natures are affected by Heisenberg's Principle; a macroscopic particle with a minute wave nature is not.

Example of the Heisenberg Uncertainty Principle

Electromagnetic radiation and tiny matter both exhibit a dual nature of mass/ momentum and wave nature. For macroscopic particles, position and velocity/momentum may both be computed concurrently.

If, for instance, it is possible to accurately detect both the position and speed of a moving automobile at the same time. For minuscule particles, it won't be possible to fix the location and detect the particle's velocity/momentum simultaneously.

Very tiny particles, such as electrons with a mass of 9.91x10^-31 kg, cannot be detected with the human eye.

• When an intense laser beam strikes an electron, the electron turns into light. This illumination aids in determining the electron's location.
• The electron's momentum increases as a result of collisions with other amplified light sources, pushing it farther from its origin.
• The particle's momentum and/or velocity would have changed from their starting states if the location hadn't been set.
• Therefore, even if a particle's location is accurate, its velocity or momentum will not be, and vice versa.
• In contrast, accurate momentum measurement will result in a change in position.

Heisenberg Uncertainty Principle Equations

An extremely precise mathematical statement that characterizes the nature of quantum systems is Heisenberg's uncertainty principle. As a result, we frequently think about the following two equations that are connected to the uncertainty principle:
1. ∆X ⋅ ∆p ~ ħ
2. ∆E ⋅ ∆t ~ ħ

Here, 
ħ = value of Planck’s constant divided by 2*pi
∆X = uncertainty in the position
∆p = uncertainty in momentum
∆E = uncertainty in the energy
∆t = uncertainty in time measurement