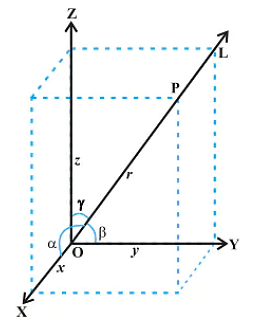
The projection of a line segment $OP$ through origin $O$, on the coordinate axes are $8, 5, 6$. Then, the length of the line segment $OP$ is equal to
- $ 5 $
- $ 5\sqrt{5} $
- $ 10\sqrt{5} $
- None of these
The Correct Option is B
Solution and Explanation
$ \therefore $ $ l=\cos \,\alpha ,\,\,\,m=\cos \beta ,\,\,n=\cos \,\gamma $
where $ \alpha ,\beta ,\gamma $
are the angles which the line segment PQ makes with the axes. Suppose length of line segment
$ PQ=r $
This, projection of line segment PQ on x-axis
$ =PQ\,\,\cos \,\alpha =rl $
Also, the projection of line segment PQ on x-axis
$ =8 $
$ \therefore $ $ lr=8 $
Similarly $ mr=5,\,\,nr=6 $
Now, on squaring adding these equations, we get
$ {{(lr)}^{2}}+{{(mr)}^{2}}+{{(nr)}^{2}}={{8}^{2}}+{{5}^{2}}+{{6}^{2}} $
$ {{r}^{2}}({{l}^{2}}+{{m}^{2}}+{{n}^{2}})=64+25+36 $
$ (\because \,\,\,\,{{l}^{2}}+{{m}^{2}}+{{n}^{2}}=1) $
$ \Rightarrow $ $ {{r}^{2}}=125 $
$ \Rightarrow $ $ r=5\sqrt{3} $
Top Questions on Three Dimensional Geometry
- If A(2,1,-1), B(6,-3,2), C(-3,12,4) are the vertices of a triangle ABC and the equation of the plane containing the triangle ABC is $53x+by+cz+d=0$, then $\frac{d}{b+c}=$
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
- If $(\alpha, \beta, \gamma)$ is the foot of the perpendicular drawn from a point $(-1,2,-1)$ to the line joining the points $(2,-1,1)$ and $(1,1,-2)$, then $\alpha+\beta+\gamma=$
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
- If m:n is the ratio in which the point $\left(\frac{8}{5}, \frac{1}{5}, \frac{8}{5}\right)$ divides the line segment joining the points (2,p,2) and (p,-2,p) where p is an integer then $\frac{3m+n}{3n}=$
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
- Let $\pi_1$ be the plane determined by the vectors $\hat{i}+\hat{j}, \hat{i}+\hat{k}$ and $\pi_2$ be the plane determined by the vectors $\hat{j}-\hat{k}, \hat{k}-\hat{i}$. Let $\vec{a}$ be a non-zero vector parallel to the line of intersection of the planes $\pi_1$ and $\pi_2$. If $\vec{b} = \hat{i}+\hat{j}-\hat{k}$ then the angle between the vectors $\vec{a}$ and $\vec{b}$ is
- TS EAMCET - 2025
- Mathematics
- Three Dimensional Geometry
Show that the following lines intersect. Also, find their point of intersection:
Line 1: \[ \frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4} \]
Line 2: \[ \frac{x - 4}{5} = \frac{y - 1}{2} = z \]
- CBSE CLASS XII - 2025
- CBSE Compartment XII - 2025
- Mathematics
- Three Dimensional Geometry
Questions Asked in JKCET exam
- 5 books in Math and 3 books in Physics are placed on a shelf so that the books on the same subject always remain together. The possible arrangements are
- JKCET - 2024
- Permutations
- If the length of a chord of a circle is equal to that of radius of the circle, then the angle subtended in radius, at the centre of the circle by the chord is
- Which of the following is a null set?
- Which of the following statement is true?
- Trans-esterification is a reaction between
- JKCET - 2024
- Organic Chemistry
Concepts Used:
Three Dimensional Geometry
Mathematically, Geometry is one of the most important topics. The concepts of Geometry are derived w.r.t. the planes. So, Geometry is divided into three major categories based on its dimensions which are one-dimensional geometry, two-dimensional geometry, and three-dimensional geometry.
Direction Cosines and Direction Ratios of Line:
Consider a line L that is passing through the three-dimensional plane. Now, x,y and z are the axes of the plane and α,β, and γ are the three angles the line makes with these axes. These are commonly known as the direction angles of the plane. So, appropriately, we can say that cosα, cosβ, and cosγ are the direction cosines of the given line L.