The magnitude of magnetic field inside a solenoid of length 0.3 m having 800 turns carrying a current of 6 A is
Show Hint
- 2.03 T
- 60.3 mT
- 20 mT
- 6.03 T
The Correct Option is C
Solution and Explanation
Step 1: Understanding the Concept:
A solenoid is a coil of wire that produces a nearly uniform magnetic field in its interior when a current is passed through it. The strength of this magnetic field depends on the number of turns per unit length, the current, and the permeability of the medium inside.
Step 2: Key Formula or Approach:
The magnitude of the magnetic field \(B\) inside a long solenoid is given by the formula:
\[ B = \mu_0 n I \]
where \(\mu_0\) is the permeability of free space (\(4\pi \times 10^{-7} \, \text{T}\cdot\text{m/A}\)), \(I\) is the current, and \(n\) is the number of turns per unit length.
The number of turns per unit length \(n\) is calculated as \(n = \frac{N}{L}\), where \(N\) is the total number of turns and \(L\) is the length of the solenoid.
Step 3: Detailed Explanation:
Given data:
Length of the solenoid, \(L = 0.3 \, \text{m}\).
Total number of turns, \(N = 800\).
Current, \(I = 6 \, \text{A}\).
Calculation:
First, calculate the number of turns per unit length, \(n\):
\[ n = \frac{N}{L} = \frac{800}{0.3} = \frac{8000}{3} \, \text{turns/m} \]
Now, substitute the values into the magnetic field formula:
\[ B = \mu_0 n I = (4\pi \times 10^{-7}) \times \left(\frac{8000}{3}\right) \times 6 \]
\[ B = (4\pi \times 10^{-7}) \times (8000 \times 2) \]
\[ B = 4\pi \times 10^{-7} \times 16000 \]
\[ B = 64000 \pi \times 10^{-7} = 6.4\pi \times 10^{-3} \, \text{T} \]
Now, we calculate the numerical value using \(\pi \approx 3.14159\):
\[ B \approx 6.4 \times 3.14159 \times 10^{-3} \, \text{T} \]
\[ B \approx 20.106 \times 10^{-3} \, \text{T} \]
This is equal to 20.106 mT. The closest option is 20 mT.
Step 4: Final Answer:
The magnitude of the magnetic field inside the solenoid is approximately 20 mT.
Top Questions on Solenoids and Toroids
- The self-inductance of a solenoid depends on
- Bihar Board XII - 2025
- Physics
- Solenoids and Toroids
- The direction of magnetic field inside a current carrying solenoid is
- Bihar Board XII - 2025
- Physics
- Solenoids and Toroids
- (i) State any two factors on which the strength of magnetic field produced by a current-carrying solenoid depends.
- UP Board X - 2025
- Science
- Solenoids and Toroids
- (i) Draw magnetic lines of force due to a current carrying solenoid.
- UP Board X - 2025
- Science
- Solenoids and Toroids
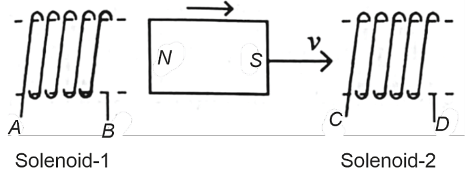
In the above diagram, a strong bar magnet is moving towards solenoid-2 from solenoid-1. The direction of induced current in solenoid-1 and that in solenoid-2, respectively, are through the directions :- NEET (UG) - 2024
- Physics
- Solenoids and Toroids
Questions Asked in CUET exam
- A person walks 10 m North, then turns right and walks 5 m, then turns right again and walks 10 m. What direction is he facing now?
- CUET (UG) - 2025
- Direction sense
- Which number will replace the question mark?
3, 6, 18, 72, ?- CUET (UG) - 2025
- Number Series
- Which of the following organelles is involved in the synthesis of proteins?
- CUET (UG) - 2025
- Cell Biology
- A man walks 10 km north, then turns right and walks 5 km, then turns right again and walks 10 km. In which direction is he now facing, and how far is he from the starting point?
- CUET (UG) - 2025
- Direction sense
- Pointing to a man, Rani says, "He is the son of my mother's only daughter.” How is the man related to Rani?
- CUET (UG) - 2025
- Blood Relations