The locus of a point which is equidistant from the points $(1,1)$ and $(3, 3)$ is
- $y = x + 4$
- $x + y = 4$
- $x = 2$
- $y = 2$
The Correct Option is B
Solution and Explanation
i.e., $ PA=PB $
$\Rightarrow\, (P A)^{2}=(P B)^{2}$
$\Rightarrow\,(h-1)^{2}+(k-1)^{2}=(h-3)^{2}+(k-3)^{2}$ (by distance formula)
$\Rightarrow 1-2 h+1-2 k=9-6 h+9-6 k$
$\Rightarrow\, 4 h+4 k=16$
$\Rightarrow\, h+k=4$
So, required locus is $x+y=4$.
Top Questions on Straight lines
- Rhombus vertices A(1,2), C(-3,-6). Line AD parallel to $7x-y=14$. Find $|\alpha+\beta+\gamma+\delta|$.
- JEE Main - 2026
- Mathematics
- Straight lines
- Let the angles made with the positive $x$-axis by two straight lines drawn from the point $P(2,3)$ and meeting the line $x+y=6$ at a distance $\sqrt{\frac{2}{3}}$ from the point $P$ be $\theta_1$ and $\theta_2$. Then the value of $(\theta_1+\theta_2)$ is
- JEE Main - 2026
- Mathematics
- Straight lines
- If two lines drawn from a point $P(2,3)$ intersect the line $x+y=6$ at a distance $\sqrt{\dfrac{2}{3}}$, then the angle between the lines is
- JEE Main - 2026
- Mathematics
- Straight lines
- If two lines drawn from a point $P(2,3)$ intersect the line $x+y=6$ at a distance $\sqrt{\dfrac{2}{3}}$, then the angle between the lines is
- JEE Main - 2026
- Mathematics
- Straight lines
- The equation of a straight line is given by \( y = 3x + 4 \). What is the slope of the line?
- BITSAT - 2025
- Mathematics
- Straight lines
Questions Asked in KEAM exam
- Which among the following has the highest molar elevation constant?
- KEAM - 2025
- Colligative Properties
- The formula of Ammonium phosphomolybdate is
- KEAM - 2025
- coordination compounds
- Which is a Lewis acid?
- KEAM - 2025
- Acids and Bases
- Hardness of water is estimated by titration with
- KEAM - 2025
- Solutions
- Which of the following gases has the lowest solubility in water at 298 K?
- KEAM - 2025
- Solutions
Concepts Used:
Straight lines
A straight line is a line having the shortest distance between two points.
A straight line can be represented as an equation in various forms, as show in the image below:
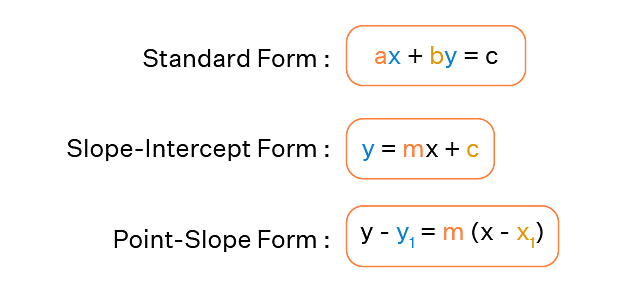
The following are the many forms of the equation of the line that are presented in straight line-
1. Slope – Point Form
Assume P0(x0, y0) is a fixed point on a non-vertical line L with m as its slope. If P (x, y) is an arbitrary point on L, then the point (x, y) lies on the line with slope m through the fixed point (x0, y0) if and only if its coordinates fulfil the equation below.
y – y0 = m (x – x0)
2. Two – Point Form
Let's look at the line. L crosses between two places. P1(x1, y1) and P2(x2, y2) are general points on L, while P (x, y) is a general point on L. As a result, the three points P1, P2, and P are collinear, and it becomes
The slope of P2P = The slope of P1P2 , i.e.
\(\frac{y-y_1}{x-x_1} = \frac{y_2-y_1}{x_2-x_1}\)
Hence, the equation becomes:
y - y1 =\( \frac{y_2-y_1}{x_2-x_1} (x-x1)\)
3. Slope-Intercept Form
Assume that a line L with slope m intersects the y-axis at a distance c from the origin, and that the distance c is referred to as the line L's y-intercept. As a result, the coordinates of the spot on the y-axis where the line intersects are (0, c). As a result, the slope of the line L is m, and it passes through a fixed point (0, c). The equation of the line L thus obtained from the slope – point form is given by
y – c =m( x - 0 )
As a result, the point (x, y) on the line with slope m and y-intercept c lies on the line, if and only if
y = m x +c