Question:
The equilibrium constant for isomerization of 1-butene to trans-2-butene at 27°C is ________ (round off to one decimal place).
The equilibrium constant for isomerization of 1-butene to trans-2-butene at 27°C is ________ (round off to one decimal place).
Show Hint
The equilibrium constant can be calculated using the relationship between Gibbs free energy change and temperature.
Updated On: Nov 25, 2025
Hide Solution
Verified By Collegedunia
Correct Answer: 28.2
Solution and Explanation
The equilibrium constant \( K \) is related to the standard Gibbs free energy change \( \Delta_r G^\circ \) by the following equation:
\[
\Delta_r G^\circ = -RT \ln K
\]
where:
- \( R \) is the gas constant \( = 8.314 \, \text{J/K mol} \),
- \( T \) is the temperature in Kelvin \( T = 27^\circ C + 273.15 = 300.15 \, \text{K} \),
- \( \Delta_r G^\circ \) is the standard Gibbs free energy change of the reaction.
Given: \[ \Delta_r G^\circ = \Delta_r G^\circ (\text{1-butene}) - \Delta_r G^\circ (\text{trans-2-butene}) = 71.39 \, \text{kJ/mol} - 63.06 \, \text{kJ/mol} = 8.33 \, \text{kJ/mol} = 8330 \, \text{J/mol} \] Now, substituting values into the equation: \[ 8330 = -8.314 \times 300.15 \times \ln K \] Solving for \( K \): \[ \ln K = \frac{-8330}{8.314 \times 300.15} = -3.34 \] \[ K = e^{-3.34} = 0.035 \] Thus, the equilibrium constant \( K \) is approximately \( 28.2 \) (rounded to one decimal place).
- \( R \) is the gas constant \( = 8.314 \, \text{J/K mol} \),
- \( T \) is the temperature in Kelvin \( T = 27^\circ C + 273.15 = 300.15 \, \text{K} \),
- \( \Delta_r G^\circ \) is the standard Gibbs free energy change of the reaction.
Given: \[ \Delta_r G^\circ = \Delta_r G^\circ (\text{1-butene}) - \Delta_r G^\circ (\text{trans-2-butene}) = 71.39 \, \text{kJ/mol} - 63.06 \, \text{kJ/mol} = 8.33 \, \text{kJ/mol} = 8330 \, \text{J/mol} \] Now, substituting values into the equation: \[ 8330 = -8.314 \times 300.15 \times \ln K \] Solving for \( K \): \[ \ln K = \frac{-8330}{8.314 \times 300.15} = -3.34 \] \[ K = e^{-3.34} = 0.035 \] Thus, the equilibrium constant \( K \) is approximately \( 28.2 \) (rounded to one decimal place).
Was this answer helpful?
0
0
Top Questions on Equilibrium constants for homogeneous reactions
- The CORRECT option(s) of Y for the following reaction is/are
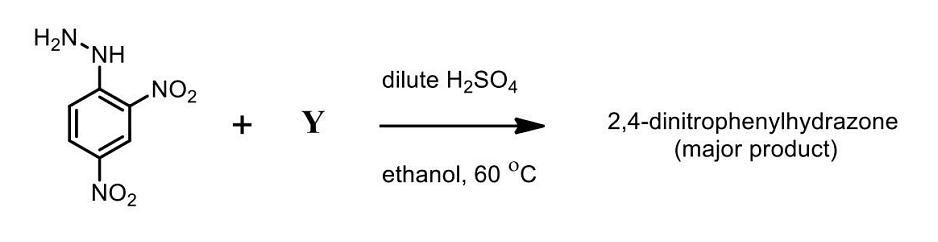
- GATE XL - 2024
- Chemistry
- Equilibrium constants for homogeneous reactions
- The CORRECT option(s) of Y for the following reaction is/are

- GATE XL - 2024
- Chemistry
- Equilibrium constants for homogeneous reactions
Questions Asked in GATE XL exam
- Which enzyme is used to join two DNA fragments in genetic engineering?
- GATE XL - 2026
- Biotechnology
- Which pyramid is always upright in an ecosystem?
- The DNA double helix is stabilized primarily by:
- The process of conversion of nitrogen into ammonia by bacteria is called:
- GATE XL - 2026
- Microbiology
- Which of the following amino acids is essential in human diet?
- GATE XL - 2026
- Biochemistry
View More Questions