The compressibility factor of an ideal gas is
- 1
- 2
- 4
- 6
The Correct Option is A
Solution and Explanation
$Z=\frac{P V}{(P V) \text { ideal }}=\frac{P V}{n R T}$
for non ideal gases, $ Z \neq 1$
for ideal gases. $Z=1$
Top Questions on Van Der Waals equation
- Molar volume ($ V_m $) of a van der Waals gas can be calculated by expressing the van der Waals equation as a cubic equation with $ V_m $ as the variable. The ratio (in mol dm$^{-3}$) of the coefficient of $ V_m^2 $ to the coefficient of $ V_m $ for a gas having van der Waals constants $ a = 6.0 \, \text{dm}^6 \, \text{atm mol}^{-2} $ and $ b = 0.060 \, \text{dm}^3 \, \text{mol}^{-1} $ at 300 K and 300 atm is ____. Use: Universal gas constant $ R = 0.082 \, \text{dm}^3 \, \text{atm mol}^{-1} \, \text{K}^{-1} $
- JEE Advanced - 2025
- Chemistry
- Van Der Waals equation
- Arrange the following gases in increasing order of van der Waals constant 'a'
A. Ar
B. CH4
C. H₂O
D. C6H6
Choose the correct option from the following.- JEE Main - 2023
- Chemistry
- Van Der Waals equation
- Which of the following statemnt is incorect for physisorption?
- GUJCET - 2023
- Chemistry
- Van Der Waals equation
- At low pressure, the van der Waal's equation is reduced to
- VITEEE - 2019
- Chemistry
- Van Der Waals equation
- If $V$ is the volume of one molecule of gas under given conditions, the van der Waal?s constant $b$ is
- BITSAT - 2018
- Chemistry
- Van Der Waals equation
Questions Asked in JEE Advanced exam
The reaction sequence given below is carried out with 16 moles of X. The yield of the major product in each step is given below the product in parentheses. The amount (in grams) of S produced is ____.

Use: Atomic mass (in amu): H = 1, C = 12, O = 16, Br = 80- JEE Advanced - 2025
- Organic Chemistry
Let $ a_0, a_1, ..., a_{23} $ be real numbers such that $$ \left(1 + \frac{2}{5}x \right)^{23} = \sum_{i=0}^{23} a_i x^i $$ for every real number $ x $. Let $ a_r $ be the largest among the numbers $ a_j $ for $ 0 \leq j \leq 23 $. Then the value of $ r $ is ________.
- JEE Advanced - 2025
- binomial expansion formula
- The total number of real solutions of the equation $$ \theta = \tan^{-1}(2 \tan \theta) - \frac{1}{2} \sin^{-1} \left( \frac{6 \tan \theta}{9 + \tan^2 \theta} \right) $$ is
(Here, the inverse trigonometric functions $ \sin^{-1} x $ and $ \tan^{-1} x $ assume values in $[-\frac{\pi}{2}, \frac{\pi}{2}]$ and $(-\frac{\pi}{2}, \frac{\pi}{2})$, respectively.)- JEE Advanced - 2025
- Inverse Trigonometric Functions
Let $ \mathbb{R} $ denote the set of all real numbers. Then the area of the region $$ \left\{ (x, y) \in \mathbb{R} \times \mathbb{R} : x > 0, y > \frac{1}{x},\ 5x - 4y - 1 > 0,\ 4x + 4y - 17 < 0 \right\} $$ is
- JEE Advanced - 2025
- Coordinate Geometry
The center of a disk of radius $ r $ and mass $ m $ is attached to a spring of spring constant $ k $, inside a ring of radius $ R>r $ as shown in the figure. The other end of the spring is attached on the periphery of the ring. Both the ring and the disk are in the same vertical plane. The disk can only roll along the inside periphery of the ring, without slipping. The spring can only be stretched or compressed along the periphery of the ring, following Hooke’s law. In equilibrium, the disk is at the bottom of the ring. Assuming small displacement of the disc, the time period of oscillation of center of mass of the disk is written as $ T = \frac{2\pi}{\omega} $. The correct expression for $ \omega $ is ( $ g $ is the acceleration due to gravity):

- JEE Advanced - 2025
- Waves and Oscillations
Concepts Used:
Van Der Waals Equation
Van der Waals equation is an equation relating the relationship between the pressure, volume, temperature, and amount of real gases.
Read More: Derivation of Van Der Waals Equation
Derivation of Van der Waals equation:
For a real gas containing ‘n’ moles, the equation is written as
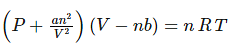
Where, P, V, T, n are the pressure, volume, temperature and moles of the gas. ‘a’ and ‘b’ constants specific to each gas.
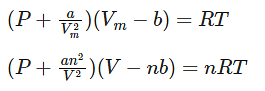
Where,
Vm: molar volume of the gas
R: universal gas constant
T: temperature
P: pressure
V: volume
Thus, Van der Waals equation can be reduced to ideal gas law as PVm = RT.
The equation can further be written as;
- Cube power of volume:
- Reduced equation (Law of corresponding states) in terms of critical constants:
Units of Van der Waals equation Constants
a: atm lit² mol-²
b: litre mol-¹