The colour of the $X_2$ molecules of group $17$ elements changes gradually from yellow to violet down the group. This is due to
- the physical state of $X_2$ at room temperature changes from gas to solid down the group
- decrease in ionization energy down the group
- decrease in $p^*-s^*$ gap down the group
- decrease in HOMO-LUMO gap down the group
The Correct Option is D
Solution and Explanation
(i) decrease in $\pi^{*}-\sigma^{*}$ gap down the group
(ii) decrease in HOMO-LUMO gap down the group
Top Questions on Molecular Orbital Theory
- Pair of species among the following having same bond order as well as paramagnetic character will be:
- JEE Main - 2026
- Chemistry
- Molecular Orbital Theory
- Among the species O$_2^+$, N$_2^-$, N$_2^{2-}$ and O$_2^-$ which have same bond order as well as paramagnetic in nature.
- JEE Main - 2026
- Chemistry
- Molecular Orbital Theory
Regarding the molecular orbital (MO) energy levels for homonuclear diatomic molecules, the INCORRECT statement(s) is (are):
- JEE Advanced - 2025
- Chemistry
- Molecular Orbital Theory
- Arrange the following in increasing order of bond order: (A) He\(_2^+\)
(B) O\(_2^-\)
(C) HF
(D) NO\(^-\)- CUET (PG) - 2025
- Chemistry
- Molecular Orbital Theory
- Which of the following is the ratio of 5\(^\text{th}\) Bohr orbit \( (r_5) \) of He\(^+\) & Li\(^{2+}\)?
- JEE Main - 2025
- Chemistry
- Molecular Orbital Theory
Questions Asked in JEE Advanced exam
- Let $ x_0 $ be the real number such that $ e^{x_0} + x_0 = 0 $. For a given real number $ \alpha $, define $$ g(x) = \frac{3xe^x + 3x - \alpha e^x - \alpha x}{3(e^x + 1)} $$ for all real numbers $ x $. Then which one of the following statements is TRUE?
- JEE Advanced - 2025
- Fundamental Theorem of Calculus
- A linear octasaccharide (molar mass = 1024 g mol$^{-1}$) on complete hydrolysis produces three monosaccharides: ribose, 2-deoxyribose and glucose. The amount of 2-deoxyribose formed is 58.26 % (w/w) of the total amount of the monosaccharides produced in the hydrolyzed products. The number of ribose unit(s) present in one molecule of octasaccharide is _____.
Use: Molar mass (in g mol$^{-1}$): ribose = 150, 2-deoxyribose = 134, glucose = 180; Atomic mass (in amu): H = 1, O = 16- JEE Advanced - 2025
- Biomolecules
Let $ P(x_1, y_1) $ and $ Q(x_2, y_2) $ be two distinct points on the ellipse $$ \frac{x^2}{9} + \frac{y^2}{4} = 1 $$ such that $ y_1 > 0 $, and $ y_2 > 0 $. Let $ C $ denote the circle $ x^2 + y^2 = 9 $, and $ M $ be the point $ (3, 0) $. Suppose the line $ x = x_1 $ intersects $ C $ at $ R $, and the line $ x = x_2 $ intersects $ C $ at $ S $, such that the $ y $-coordinates of $ R $ and $ S $ are positive. Let $ \angle ROM = \frac{\pi}{6} $ and $ \angle SOM = \frac{\pi}{3} $, where $ O $ denotes the origin $ (0, 0) $. Let $ |XY| $ denote the length of the line segment $ XY $. Then which of the following statements is (are) TRUE?
- JEE Advanced - 2025
- Conic sections
- Adsorption of phenol from its aqueous solution on to fly ash obeys Freundlich isotherm. At a given temperature, from 10 mg g$^{-1}$ and 16 mg g$^{-1}$ aqueous phenol solutions, the concentrations of adsorbed phenol are measured to be 4 mg g$^{-1}$ and 10 mg g$^{-1}$, respectively. At this temperature, the concentration (in mg g$^{-1}$) of adsorbed phenol from 20 mg g$^{-1}$ aqueous solution of phenol will be ____. Use: $\log_{10} 2 = 0.3$
- JEE Advanced - 2025
- Adsorption
- At 300 K, an ideal dilute solution of a macromolecule exerts osmotic pressure that is expressed in terms of the height (h) of the solution (density = 1.00 g cm$^{-3}$) where h is equal to 2.00 cm. If the concentration of the dilute solution of the macromolecule is 2.00 g dm$^{-3}$, the molar mass of the macromolecule is calculated to be $X \times 10^{4}$ g mol$^{-1}$. The value of $X$ is ____. Use: Universal gas constant (R) = 8.3 J K$^{-1}$ mol$^{-1}$ and acceleration due to gravity (g) = 10 m s$^{-2}\}$
- JEE Advanced - 2025
- Colligative Properties
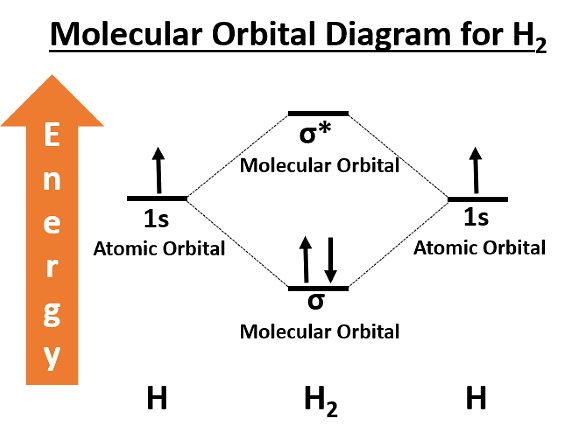
Concepts Used:
Molecular Orbital Theory
The Molecular Orbital Theory is a more sophisticated model of chemical bonding where new molecular orbitals are generated using a mathematical process called Linear Combination of Atomic Orbitals (LCAO).
Molecular Orbital theory is a chemical bonding theory that states that individual atoms combine together to form molecular orbitals. Due to this arrangement in MOT Theory, electrons associated with different nuclei can be found in different atomic orbitals. In molecular orbital theory, the electrons present in a molecule are not assigned to individual chemical bonds between the atoms. Rather, they are treated as moving under the influence of the atomic nuclei in the entire molecule.