The area of the region satisfying the inequalities \(|x|-y≤1,y≥0\) and \(y≤1\) is [This Question was asked as TITA]
- 3 Square units
- 2 Square units
- 5 Square units
- 4 Square units
The Correct Option is A
Approach Solution - 1
The graph of \(|x|-y≤1,y≥0\) and \(y≤1\) is as follows: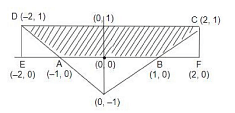
To find the area of quadrilateral ABCD, we subtract the areas of triangles EAD and BFC from the area of rectangle EFCD:
Area of ABCD = Area of EFCD − Area of △EAD − Area of △BFC
Using the formula:
\( \text{Area of ABCD} = EF \times FC - \frac{1}{2} \times EA \times ED - \frac{1}{2} \times BF \times FC \)
Substituting the values:
\( = 4 \times 1 - \frac{1}{2} \times 1 \times 1 - \frac{1}{2} \times 1 \times 1 \)
\( = 4 - 0.5 - 0.5 = 3 \) square units
Final Answer: \( \boxed{3} \) square units
Approach Solution -2
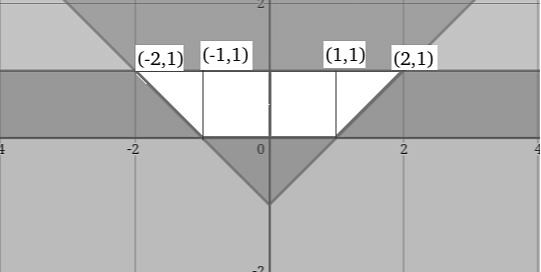
Area of the region contained by the lines | x | -y ≤ 1, y ≥ 0 and y ≤ 1 is the two triangle and the one rectangle in white region.
So, we have calculate these area to get the total area.
Total Area = Area of rectangle + 2 × Area of triangle
= \(2+(\frac{1}{2}\times2\times1)=3\)
Therefore, the correct option is (A) : 3 Square units.
Top Questions on Geometry
- If \[ \lim_{x \to 0} \frac{e^{a(x-1)} + 2\cos(bx) + e^{-x}(c - 1)}{x \cos x - \ln(1 + x)} = 2, \] Then the value of \( a^2 + b^2 + c^2 \) is:
- If \( P(10, 2\sqrt{15}) \) lies on the hyperbola \( \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \) and the length of the latus rectum is 8, then the square of the area of \( \Delta PS_1S_2 \) is [where \( S_1 \) and \( S_2 \) are the foci of the hyperbola].
- If \( \cos(\alpha + \beta) = -\frac{1}{10} \) and \( \sin(\alpha - \beta) = \frac{3}{8} \), where \[ 0<\alpha<\frac{\pi}{3} \quad \text{and} \quad 0<\beta<\frac{\pi}{4}, \] and \[ \tan(2\alpha) = \frac{3\left(1 - \sqrt{55}\right)}{\sqrt{11} \left(s + \sqrt{5}\right)}, \] and \( r, s \in \mathbb{N} \), then \( r^2 + s \) is:
- If \( O \) is the vertex of the parabola \( x^2 = 4y \), \( Q \) is a point on the parabola. If \( C \) is the locus of a point which divides \( OQ \) in the ratio \( 2:3 \), then the equation of the chord of \( C \) which is bisected at the point \( (1,2) \) is:
- The locus of the point of intersection of tangents drawn to the circle \[ (x - 2)^2 + (y - 3)^2 = 16, \] which subtends an angle of \(120^\circ\), is:
Questions Asked in CAT exam
- The passage given below is followed by four summaries. Choose the option that best captures the essence of the passage.
In the dynamic realm of creativity, artists often find themselves at the crossroads between drawing inspiration from diverse cultures and inadvertently crossing into the territory of cultural appropriation. Inspiration is the lifeblood of creativity, driving artists to create works that resonate across borders. In a globalized era of the modern world, artists draw from a vast array of cultural influences. When approached respectfully, inspiration becomes a bridge, fostering understanding and appreciation of cultural diversity. However, the line between inspiration and cultural appropriation can be thin and easily blurred.
Cultural appropriation occurs when elements from a particular culture are borrowed without proper understanding, respect, or acknowledgment. This leads to the commodification of sacred symbols, the reinforcement of stereotypes, and the erasure of the cultural context from which these elements originated. It is essential to recognize that the impact of cultural appropriation extends beyond the realm of artistic expression, influencing societal perceptions and perpetuating power imbalances.- CAT - 2025
- Para Summary
- The number of distinct integers $n$ for which $\log_{\left(\frac14\right)}(n^2 - 7n + 11)>0$ is:
- CAT - 2025
- Linear Inequalities
- In the set of consecutive odd numbers $\{1, 3, 5, \ldots, 57\}$, there is a number $k$ such that the sum of all the elements less than $k$ is equal to the sum of all the elements greater than $k$. Then, $k$ equals?
- CAT - 2025
- Number Systems
- The number of distinct pairs of integers $(x, y)$ satisfying the inequalities $x>y \ge 3$ and $x + y<14$ is:
- CAT - 2025
- Number Systems
For any natural number $k$, let $a_k = 3^k$. The smallest natural number $m$ for which \[ (a_1)^1 \times (a_2)^2 \times \dots \times (a_{20})^{20} \;<\; a_{21} \times a_{22} \times \dots \times a_{20+m} \] is:
- CAT - 2025
- Linear Inequalities