Comprehension
Staff employed in a UNESCO office in Paris are represented by four intersecting circles as in the given diagram. Each circle represents people who can read and write English, French, Spanish and Russian. Strength of people in each circle is also shown alongside. Study the diagram to answer the questions that follow.
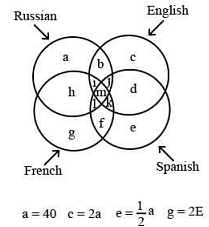

Question: 1
How many people know only Spanish ?
How many people know only Spanish ?
Updated On: Sep 2, 2025
- 10
- 20
- 40
- 60
Hide Solution
Verified By Collegedunia
The Correct Option is B
Solution and Explanation
Step 1 — Map the labels: In the four-circle Venn diagram, the single-language regions are labeled as follows: Russian-only = a, English-only = c, Spanish-only = e, French-only = g. The overlapping parts are labeled with other letters (b, d, f, h, m, n), but they aren’t needed for this question because “only Spanish” refers strictly to region e.
Step 2 — Use the given values/relations:
We are told: a = 40, c = 2a, e = (1/2)·a, g = 2e.
These relations connect the single-language counts to one another using a as the reference.
Step 3 — Compute e (Spanish-only):
Since a = 40, then
e = (1/2)·a = (1/2)·40 = 20.
Step 4 — Interpret the result: The value e is exactly the count of staff who belong to the Spanish circle and to no other circle, i.e., who know only Spanish.
Answer: 20 people know only Spanish.
Step 2 — Use the given values/relations:
We are told: a = 40, c = 2a, e = (1/2)·a, g = 2e.
These relations connect the single-language counts to one another using a as the reference.
Step 3 — Compute e (Spanish-only):
Since a = 40, then
e = (1/2)·a = (1/2)·40 = 20.
Step 4 — Interpret the result: The value e is exactly the count of staff who belong to the Spanish circle and to no other circle, i.e., who know only Spanish.
Answer: 20 people know only Spanish.
Was this answer helpful?
0
0
Question: 2
How many people can read and write any one language except French ?
How many people can read and write any one language except French ?
Updated On: Sep 2, 2025
100
- 160
- 140
- 120
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
Step 1 — Interpret the question:
We are asked to find the number of people who know only one language, but that language must not be French. This means we need to count:
- Russian-only (a)
- English-only (c)
- Spanish-only (e)
We do not include French-only (g) because the question says “except French.”
Step 2 — Recall the given relations:
We are told:
a = 40
c = 2a
e = (1/2)·a
g = 2e
Step 3 — Calculate each required value:
- Russian-only (a) = 40
- English-only (c) = 2a = 2 × 40 = 80
- Spanish-only (e) = (1/2) × 40 = 20
Step 4 — Add them together:
Total = a + c + e = 40 + 80 + 20 = 140
Step 5 — Final interpretation:
Therefore, the number of people who can read and write only one language, excluding French, is 140.
Answer: The correct option is (C) : 140.
We are asked to find the number of people who know only one language, but that language must not be French. This means we need to count:
- Russian-only (a)
- English-only (c)
- Spanish-only (e)
We do not include French-only (g) because the question says “except French.”
Step 2 — Recall the given relations:
We are told:
a = 40
c = 2a
e = (1/2)·a
g = 2e
Step 3 — Calculate each required value:
- Russian-only (a) = 40
- English-only (c) = 2a = 2 × 40 = 80
- Spanish-only (e) = (1/2) × 40 = 20
Step 4 — Add them together:
Total = a + c + e = 40 + 80 + 20 = 140
Step 5 — Final interpretation:
Therefore, the number of people who can read and write only one language, excluding French, is 140.
Answer: The correct option is (C) : 140.
Was this answer helpful?
0
0
Question: 3
People who can read and write all the language except Spanish, are represented by
People who can read and write all the language except Spanish, are represented by
Updated On: Sep 2, 2025
- k
- g
- b
- i
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
Step 1 — Understand the question:
We need to identify the region in the Venn diagram that represents people who know all the languages except Spanish. This means such people know:
- Russian
- English
- French
but not Spanish.
Step 2 — Analyze the diagram:
In a four-circle Venn diagram labeled with a, b, c, d, e, f, g, h, m, n, i, etc., the specific region where Russian, English, and French overlap but Spanish is excluded is marked by the label i.
Step 3 — Interpret the representation:
Thus, the set of people who can read and write all the languages except Spanish is represented by i in the diagram.
Answer: The correct option is (D) : i.
We need to identify the region in the Venn diagram that represents people who know all the languages except Spanish. This means such people know:
- Russian
- English
- French
but not Spanish.
Step 2 — Analyze the diagram:
In a four-circle Venn diagram labeled with a, b, c, d, e, f, g, h, m, n, i, etc., the specific region where Russian, English, and French overlap but Spanish is excluded is marked by the label i.
Step 3 — Interpret the representation:
Thus, the set of people who can read and write all the languages except Spanish is represented by i in the diagram.
Answer: The correct option is (D) : i.
Was this answer helpful?
0
0
Question: 4
People who cannot read and write Russian, English and French, are represented by :
People who cannot read and write Russian, English and French, are represented by :
Updated On: Sep 2, 2025
- l
- j
- h
- e
Hide Solution
Verified By Collegedunia
The Correct Option is D
Solution and Explanation
Step 1 — Carefully understand the problem statement:
The question asks: "People who cannot read and write Russian, English and French, are represented by :".
This means we are looking for individuals who are not part of the Russian circle, not part of the English circle, and not part of the French circle. In other words, they must lie completely outside these three language sets.
Step 2 — Think about what this implies in terms of the Venn diagram:
In the four-circle Venn diagram, each circle represents knowledge of one language:
- Russian
- English
- French
- Spanish
If a person is outside Russian, English, and French, the only possible language they could still belong to is the Spanish circle. Therefore, the region we are trying to identify is the portion of the Spanish circle that does not overlap with any of the other three circles.
Step 3 — Locate the correct labeled region:
From the labels given in the diagram, the part of the Spanish circle that is unique to Spanish — i.e., Spanish-only — is represented by the region e.
This is because:
- Region e = Spanish-only (no Russian, no English, no French).
- All other Spanish-related regions (like overlaps with Russian, English, or French) would involve knowledge of at least one of those three languages, which the question specifically forbids.
Step 4 — Conclude with the reasoning:
Hence, the group of people who cannot read and write Russian, English, and French must belong exclusively to the Spanish-only region. This is exactly represented by e in the diagram.
Final Answer:
The people who cannot read and write Russian, English, and French are represented by region e.
Therefore, the correct option is (D) : e.
The question asks: "People who cannot read and write Russian, English and French, are represented by :".
This means we are looking for individuals who are not part of the Russian circle, not part of the English circle, and not part of the French circle. In other words, they must lie completely outside these three language sets.
Step 2 — Think about what this implies in terms of the Venn diagram:
In the four-circle Venn diagram, each circle represents knowledge of one language:
- Russian
- English
- French
- Spanish
If a person is outside Russian, English, and French, the only possible language they could still belong to is the Spanish circle. Therefore, the region we are trying to identify is the portion of the Spanish circle that does not overlap with any of the other three circles.
Step 3 — Locate the correct labeled region:
From the labels given in the diagram, the part of the Spanish circle that is unique to Spanish — i.e., Spanish-only — is represented by the region e.
This is because:
- Region e = Spanish-only (no Russian, no English, no French).
- All other Spanish-related regions (like overlaps with Russian, English, or French) would involve knowledge of at least one of those three languages, which the question specifically forbids.
Step 4 — Conclude with the reasoning:
Hence, the group of people who cannot read and write Russian, English, and French must belong exclusively to the Spanish-only region. This is exactly represented by e in the diagram.
Final Answer:
The people who cannot read and write Russian, English, and French are represented by region e.
Therefore, the correct option is (D) : e.
Was this answer helpful?
0
0
Question: 5
People who cannot read and write Spanish and French but are conversant with English and Russian are represented by :
People who cannot read and write Spanish and French but are conversant with English and Russian are represented by :
Updated On: Sep 2, 2025
- b
- j
- m
- k
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
Step 1 — Interpret the question carefully:
The problem is asking us to find the group of people who:
- Cannot read and write Spanish
- Cannot read and write French
- But can read and write English and Russian
This means we are searching for the region in the four-circle Venn diagram where the English and Russian circles overlap, while at the same time excluding the Spanish and French circles.
Step 2 — Translate into Venn diagram logic:
- "Conversant with English and Russian" → We must look at the overlapping region between English and Russian circles.
- "Cannot read and write Spanish" → So we must exclude any overlap with the Spanish circle.
- "Cannot read and write French" → We must also exclude any overlap with the French circle.
Therefore, the required group is the part of the intersection of English ∩ Russian that does not intersect with Spanish or French.
Step 3 — Identify the correct labeled region:
In the given Venn diagram labeling, the region representing people who know both English and Russian, but do not know Spanish or French, is denoted by the letter b.
Step 4 — Explain why other regions are excluded:
- If we had chosen the English ∩ Russian ∩ Spanish overlap, then Spanish knowledge would be included, which is not allowed.
- If we had chosen the English ∩ Russian ∩ French overlap, then French knowledge would be included, which is not allowed.
- If we had chosen the English ∩ Russian ∩ Spanish ∩ French overlap, then both Spanish and French would be included, which again contradicts the condition.
Thus, the only correct region is b.
Step 5 — Final conclusion:
The region that represents people who cannot read and write Spanish and French but are conversant with English and Russian is b.
Answer: The correct option is (A) : b.
The problem is asking us to find the group of people who:
- Cannot read and write Spanish
- Cannot read and write French
- But can read and write English and Russian
This means we are searching for the region in the four-circle Venn diagram where the English and Russian circles overlap, while at the same time excluding the Spanish and French circles.
Step 2 — Translate into Venn diagram logic:
- "Conversant with English and Russian" → We must look at the overlapping region between English and Russian circles.
- "Cannot read and write Spanish" → So we must exclude any overlap with the Spanish circle.
- "Cannot read and write French" → We must also exclude any overlap with the French circle.
Therefore, the required group is the part of the intersection of English ∩ Russian that does not intersect with Spanish or French.
Step 3 — Identify the correct labeled region:
In the given Venn diagram labeling, the region representing people who know both English and Russian, but do not know Spanish or French, is denoted by the letter b.
Step 4 — Explain why other regions are excluded:
- If we had chosen the English ∩ Russian ∩ Spanish overlap, then Spanish knowledge would be included, which is not allowed.
- If we had chosen the English ∩ Russian ∩ French overlap, then French knowledge would be included, which is not allowed.
- If we had chosen the English ∩ Russian ∩ Spanish ∩ French overlap, then both Spanish and French would be included, which again contradicts the condition.
Thus, the only correct region is b.
Step 5 — Final conclusion:
The region that represents people who cannot read and write Spanish and French but are conversant with English and Russian is b.
Answer: The correct option is (A) : b.
Was this answer helpful?
0
0
Top Questions on Venn Diagrams
- In the following diagram, the square represents women, triangle represents corporate managers and circle represents MBAs. Which numbered part represents - women who are corporate managers and has done MBA as well?

- CMAT - 2025
- Logical Reasoning
- Venn Diagrams
- Atal Academy focuses on the performing arts. In the current batch, 40 students can sing, 60 students can dance and 24 students can act. No student is a triple threat (some one who can sing, dance and act). However, 16 students can sing as well as dance, 12 students can dance and act and 8 students can sing and act. How many students have only one performing talent?
- CMAT - 2025
- Logical Reasoning
- Venn Diagrams
- In an MBA entrance exam, 55% failed in QA, & 45% failed in VA, and 25% pass in both QA & VA. Find the % of students who failed in both the subjects.
- Suppose that C represents the set of all countries, R represents the set of all countries that have at least one river flowing through it, M represents the set of all countries that have at least one mountain in it, and D represents the set of all countries that have at least one desert in it. It is given that \( (R \cup M \cup D) = C \). Which one of the following gives the set of all countries that have either a mountain or a river, but does not have a desert in it? The notation \( D^c \) represents the complement of the set D with respect to the universal set C.
- NIMCET - 2025
- Mathematics
- Venn Diagrams
- Which of the following diagram indicates the best relation between Teacher, Writer and Dancer?
- CUET (UG) - 2025
- Logical Reasoning
- Venn Diagrams
View More Questions
Questions Asked in SNAP exam
- Find the unit digit of 1! + 2! + .... + 100!
- SNAP - 2025
- Number Systems
- If there are two red and blue dice. Find the probability when the sum of the dice is a prime number, where the number on red is more than blue.
- SNAP - 2025
- Probability
- A solid metallic cylinder of radius \( 6 \, \text{cm} \) and height \( 20 \, \text{cm} \) is melted and recast into a large sphere. What is the radius of the sphere?
- SNAP - 2025
- Mensuration
- A shopkeeper marks up his goods by 40% and offers a discount of 10%. What is his final profit percentage?
- SNAP - 2025
- Profit and Loss
- The political opinion piece in the newspaper was a __________ critique of the government's foreign policy, aiming to __________ a strong public reaction.
- SNAP - 2025
- Fill in the Blanks
View More Questions