Solution of (1+xy) y dx+ (1-xy)x dy=0 is?
Solution of (1+xy) y dx+ (1-xy)x dy=0 is?
Solution and Explanation
The solution to the differential equation (1+xy) y dx + (1-xy) x dy = 0 is x^2 + y^2 = c, where c is a constant.
Top Questions on Differential equations
- If \[\frac{dx}{dy} = \frac{1 + x - y^2}{y}, \quad x(1) = 1,\]then $5x(2)$ is equal to:
- JEE Main - 2024
- Mathematics
- Differential equations
- Let $\alpha$ be a non-zero real number. Suppose $f : \mathbb{R} \to \mathbb{R}$ is a differentiable function such that $f(0) = 2$ and \[\lim_{x \to \infty} f(x) = 1.\]If $f'(x) = \alpha f(x) + 3$, for all $x \in \mathbb{R}$, then $f(-\log 2)$ is equal to ________ .
- JEE Main - 2024
- Mathematics
- Differential equations
- Let\(f(x) = |2x^2 + 5|x - 3|, x \in \mathbb{R}\). If \(m\) and \(n\) denote the number of points were \(f\)is not continuous and not differentiable respectively, then\(m + n\)is equal to:
- JEE Main - 2024
- Mathematics
- Differential equations
- Let \( y = y(x) \) be the solution of the differential equation \[\left( 1 + x^2 \right) \frac{dy}{dx} + y = e^{\tan^{-1}x}, \, y(1) = 0.\]Then \( y(0) \) is:
- JEE Main - 2024
- Mathematics
- Differential equations
- Let \( y = y(x) \) be the solution of the differential equation \[\left( 2x \log_e x \right) \frac{dy}{dx} + 2y = \frac{3}{x} \log_e x, \, x>0 \, \text{and} \, y(e^{-1}) = 0.\] Then, \( y(e) \) is equal to:
- JEE Main - 2024
- Mathematics
- Differential equations
Questions Asked in MHT CET exam
- Two monkeys off mass 10 kg and 8 kg are moving along a vertical light rope the former climbing up with an acceleration of 2 m/second square while the latter coming down with a uniform velocity of 2 m/sec square find the tension in the rope at the fixed support
- MHT CET - 2024
- tension
- Which disease is primarily spread by female Anopheles mosquitoes?
- MHT CET - 2024
- HIV and AIDS
- Total genetic content of an organism is called
- MHT CET - 2024
- Non-Mendelian Genetics
- How many ATP molecules are needed as an initial investment in the glycolytic cycle (normal glycolysis)?
- MHT CET - 2024
- Glycolysis
- If \(A=\begin{bmatrix} 2a & -3b\\ 3 & 2\end{bmatrix}\) and \(\text{adj}A = AA^T\), then 2a+3b is?
- MHT CET - 2023
- Matrices
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
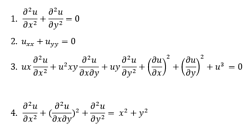
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
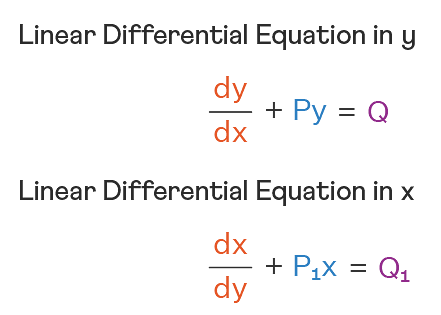
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations