Question

Make a diagram to show how hypermetropia is corrected. The near point of a hypermetropic eye is 1 m. What is the power of the lens required to correct this defect? Assume that the near point of the normal eye is 25 cm.

Answer 1

A person suffering from hypermetropia can see distinct objects clearly but faces difficulty in seeing nearby objects clearly. It happens because the eye lens focuses the incoming divergent rays beyond the retina. This defect of vision is corrected by using a convex lens. A convex lens of suitable power converges the incoming light in such a way that the image is formed on the retina, as shown in the following figure.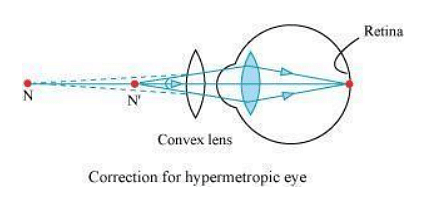

The convex lens actually creates a virtual image of a nearby object (N’ in the figure) at the near point of vision (N) of the person suffering from hypermetropia. 
The given person will be able to clearly see the object kept at 25 cm (near point of the normal eye), if the image of the object is formed at his near point, which is given as 1 m. 

Object distance, u = −25 cm 
Image distance, v = −1 m = −100 m 
Focal length, f
Using the lens formula,
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)

\(\frac{1}{-100}-\frac{1}{-25}=\frac{1}{f}\)

\(⇒\frac{1}{f}=\frac{1}{25}-\frac{1}{100}\)

\(⇒\frac{1}{f}=\frac{4-1}{100}\)

\(⇒f=\frac{100}{3}=33.3\) cm
\(=0.33\) m

\(∴\text{Power,P}=\frac{1}{f}\text{(in metres)}\)
\(=\frac{1}{0.33}=+3.0\) D
A convex lens of power +3.0 D is required to correct the defect.