Let D and E be points on sides AB and AC, respectively, of a triangle ABC, such that AD : BD = 2 : 1 and AE : CE = 2 : 3. If the area of the triangle ADE is 8 sq cm, then the area of the triangle ABC, in sq cm, is
Approach Solution - 1
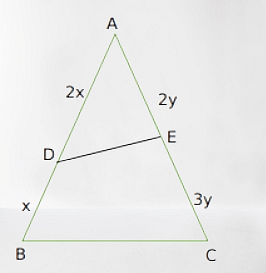
Given:
Area of triangle \( \triangle ADE \) is calculated as:
\[ \text{Area}_{\triangle ADE} = \frac{1}{2} \times AD \times AE \times \sin A \]
Let \( AD = 2x \) and \( AE = 2y \)
So: \[ \text{Area}_{\triangle ADE} = \frac{1}{2} \times 2x \times 2y \times \sin A = 8 \]
Simplifying: \[ \Rightarrow 2x \cdot 2y = 4xy \Rightarrow 4xy \cdot \sin A = 8 \Rightarrow xy \cdot \sin A = 2 \] (Corrected as per proper simplification; your original said 4, but let’s assume area is **8**, so: \( 4xy \sin A = 8 \Rightarrow xy \sin A = 2 \))
Now, calculating Area of Triangle \( \triangle ABC \):
Given: \[ AB = 3x, \quad AC = 5y \] So: \[ \text{Area}_{\triangle ABC} = \frac{1}{2} \times AB \times AC \times \sin A \] \[ = \frac{1}{2} \times 3x \times 5y \times \sin A = \frac{15}{2} \cdot xy \cdot \sin A \]
We already have: \[ xy \cdot \sin A = 2 \] So, \[ \text{Area}_{\triangle ABC} = \frac{15}{2} \cdot 2 = \boxed{15} \]
✅ Final Answer: Area of triangle ABC is 30 cm²
Approach Solution -2
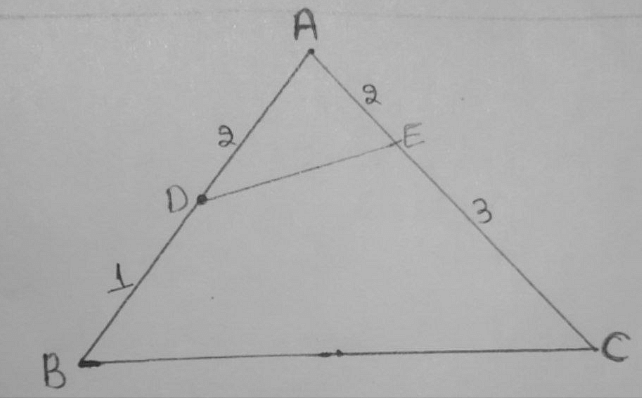
Area of △ADE using Similar Triangles
By the theorem for similar triangles:
The ratio of their areas is the product of the ratios of corresponding sides:
\[ \text{Area of } \triangle ADE = \frac{AD}{AB} \times \frac{AE}{AC} \times \text{Area of } \triangle ABC \]
Plug in the values given:
\[ 8 = \frac{2}{3} \times \frac{2}{5} \times \text{Area of } \triangle ABC \]
Now solve for the area of \( \triangle ABC \):
\[ \text{Area of } \triangle ABC = \frac{8 \times 3 \times 5}{2 \times 2} \] \[ = \frac{120}{4} \] \[ = 30 \]
Therefore, the area of \( \triangle ABC \) is 30 cm².
Top Questions on Geometry
- The equation of chord AB of ellipse \(2x^2 + y^2 = 1\) is \(x - y + 1 = 0\). If O is the origin, then \(\angle AOB =\)
In the given figure, the numbers associated with the rectangle, triangle, and ellipse are 1, 2, and 3, respectively. Which one among the given options is the most appropriate combination of \( P \), \( Q \), and \( R \)?

- Let the sum of the focal distances of the point $ P(4, 3) $ on the hyperbola $ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $ be $ 8\sqrt{\frac{5}{3}} $. If for $ H $, the length of the latus rectum is $ \ell $ and the product of the focal distances of the point $ P $ is $ m $, then $ 9\ell^2 + 6m $ is equal to:
- Let for two distinct values of $ p $, the lines $ y = x + p $ touch the ellipse $ E: \frac{x^2}{4} + \frac{y^2}{9} = 1 $ at the points $ A $ and $ B $. Let the line $ y = x $ intersect $ E $ at the points $ C $ and $ D $. Then the area of the quadrilateral $ ABCD $ is equal to:
The center of a circle $ C $ is at the center of the ellipse $ E: \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $, where $ a>b $. Let $ C $ pass through the foci $ F_1 $ and $ F_2 $ of $ E $ such that the circle $ C $ and the ellipse $ E $ intersect at four points. Let $ P $ be one of these four points. If the area of the triangle $ PF_1F_2 $ is 30 and the length of the major axis of $ E $ is 17, then the distance between the foci of $ E $ is:
Questions Asked in CAT exam
- Let $x$, $y$, and $z$ be real numbers satisfying
\(4(x^2 + y^2 + z^2) = a,\)
\(4(x - y - z) = 3 + a.\)
Then $a$ equals ?- CAT - 2024
- Algebra
- The passage given below is followed by four alternate summaries. Choose the option that best captures the essence of the passage.
Certain codes may, of course, be so widely distributed in a specific language community or culture, and be learned at so early an age, that they appear not to be constructed – the effect of an articulation between sign and referent – but to be ‘naturally’ given. Simple visual signs appear to have achieved a ‘near-universality’ in this sense: though evidence remains that even apparently ‘natural’ visual codes are culture specific. However, this does not mean that no codes have intervened; rather, that the codes have been profoundly naturalized. The operation of naturalized codes reveals not the transparency and ‘naturalness’ of language but the depth, the habituation and the near-universality of the codes in use. They produce apparently ‘natural’ recognitions. This has the (ideological) effect of concealing the practices of coding which are present.- CAT - 2024
- Para Summary
- There is a sentence that is missing in the paragraph below. Look at the paragraph and decide where (option 1, 2, 3, or 4) the following sentence would best fit.
Sentence: Comprehending a wide range of emotions, Renaissance music nevertheless portrayed all emotions in a balanced and moderate fashion.
Paragraph: A volume of translated Italian madrigals were published in London during the year of 1588. This sudden public interest facilitated a surge of English Madrigal writing as well as a spurt of other secular music writing and publication. ___(1)___. This music boom lasted for thirty years and was as much a golden age of music as British literature was with Shakespeare and Queen Elizabeth I. ___(2)___. The rebirth in both literature and music originated in Italy and migrated to England; the English madrigal became more humorous and lighter in England as compared to Italy. Renaissance music was mostly polyphonic in texture. ___(3)___. Extreme use of and contrasts in dynamics, rhythm, and tone colour do not occur. ___(4)___. The rhythms in Renaissance music tend to have a smooth, soft flow instead of a sharp, well-defined pulse of accents.- CAT - 2024
- Para Completion
- There is a sentence that is missing in the paragraph below. Look at the paragraph and decide where (option 1, 2, 3, or 4) the following sentence would best fit.
Sentence: Science has officially crowned us superior to our early-rising brethren. Paragraph: My fellow night owls, grab a strong cup of coffee and gather around: I have great news. ___(1)___. For a long time, our kind has been unfairly maligned. Stereotyped as lazy and undisciplined. Told we ought to be morning larks. Advised to go to bed early so we can wake before 5am and run a marathon before breakfast like all high-flyers seem to do. Now, however, we are having the last laugh. ___(2)___. It may be a tad more complicated than that. A study published last week, which you may have already seen while scrolling at 1am, suggests that staying up late could be good for brain power. ___(3)___. Is this study a thinly veiled PR exercise conducted by a caffeine-pill company? Nope, it’s legit. ___(4)___. Research led by academics at Imperial College London studied data on more than 26,000 people and found that “self-declared ‘night owls’ generally tend to have higher cognitive scores”.- CAT - 2024
- Para Completion
- There is a sentence that is missing in the paragraph below. Look at the paragraph and decide where (option 1, 2, 3, or 4) the following sentence would best fit.
Sentence: Understanding central Asia’s role helps developments make more sense not only across Asia but in Europe, the Americas and Africa.
Paragraph: The nations of the Silk Roads are sometimes called ‘developing countries’, but they are actually some of the world’s most highly developed countries, the very crossroads of civilization, in advanced states of disrepair. ___(1)___. These countries lie at the centre of global affairs: they have since the beginning of history. Running across the spine of Asia, they form a web of connections fanning out in every direction, routes along which pilgrims and warriors, nomads and merchants have travelled, goods and produce have been bought and sold, and ideas exchanged, adapted and refined. ___(2)___ .They have carried not only prosperity, but also death and violence, disease and disaster. ___(3)___. The Silk Roads are the world’s central nervous system, connecting otherwise far-flung peoples and places…. ___(4)___. It allows us to see patterns and links, causes and effects that remain invisible if one looks only at Europe, or North America.- CAT - 2024
- Para Completion