Equilibrium constants K1 and K2 for the following equilibria: NO(g)+\(\bigg(\frac{1}{2}\bigg)\)O2 \(^{K_1}_\rightleftharpoons\) NO2(g) and 2NO2(g) \(^{K_2}_\rightleftharpoons\) 2NO(g)+O2(g) are related as:
\(K_2\) = \(\frac{1}{K_1}\)
K2 = \(K^2_1\)
K2 = \(K^1_2\)
K2 = \(\frac{1}{K^2_1}\)
The Correct Option is D
Solution and Explanation
By changing the first reaction in reverse order and multiplying it by 2 we will get the equation similar to second equation.
Thus, K1 and K2 can be related in the above equations as:
K2 = \(\frac{1}{K^2_1}\)
\(\Rightarrow\) K1 = \(\frac{1}{\sqrt K_2}\)
Therefore, the correct option is (D): K2 = \(\frac{1}{K^2_1}\)
Top Questions on Equilibrium
- In the reaction \( \mathrm{N_2(g)} + 3\mathrm{H_2(g)} \leftrightarrow 2\mathrm{NH_3(g)} \), if the equilibrium constant \( K_c = 4 \times 10^{-3} \) at a certain temperature, which of the following is true about the reaction at equilibrium?
- BITSAT - 2025
- Chemistry
- Equilibrium
- A vessel at 1000 K contains \( \text{CO}_2 \) with a pressure of 0.5 atm. Some of \( \text{CO}_2 \) is converted into \( \text{CO} \) on addition of graphite. If total pressure at equilibrium is 0.8 atm, then \( K_p \) is:
- JEE Main - 2025
- Chemistry
- Equilibrium
- In which of the following \( K_c = K_p \)? a) \( \text{PCl}_5(g) \rightleftharpoons \text{PCl}_3(g) + \text{Cl}_2(g) \) b) \( \text{H}_2(g) + \text{I}_2(g) \rightleftharpoons 2\text{HI}(g) \)
- KEAM - 2025
- Chemistry
- Equilibrium
x mg of Mg(OH)$_2$ (molar mass = 58) is required to be dissolved in 1.0 L of water to produce a pH of 10.0 at 298 K. The value of x is ____ mg. (Nearest integer) (Given: Mg(OH)$_2$ is assumed to dissociate completely in H$_2$O)
- JEE Main - 2025
- Chemistry
- Equilibrium
- For the reaction \( \text{N}_2 (\text{g}) + 3\text{H}_2 (\text{g}) \rightleftharpoons 2\text{NH}_3 (\text{g}) \), the equilibrium constant \( K_c \) is \( 4.0 \times 10^{-2} \) at a certain temperature. If the equilibrium concentrations are \( [\text{N}_2] = 0.5 \, \text{M} \) and \( [\text{H}_2] = 1.5 \, \text{M} \), what is the equilibrium concentration of \( \text{NH}_3 \)?
- MHT CET - 2025
- Chemistry
- Equilibrium
Questions Asked in NEET exam
- De-Broglie wavelength of an electron orbiting in the \(n = 2\) state of hydrogen atom is close to (Given Bohr radius = 0.052 nm):
- NEET (UG) - 2025
- de broglie hypothesis
- Which chromosome in the human genome has the highest number of genes?
- NEET (UG) - 2025
- Human genome
- In a certain camera, a combination of four similar thin convex lenses are arranged axially in contact. Then the power of the combination and the total magnification in comparison to one lens will be, respectively:
- NEET (UG) - 2025
- Images Formed By Lenses
AB is a part of an electrical circuit (see figure). The potential difference \(V_A - V_B\), at the instant when current \(i = 2\) A and is increasing at a rate of 1 amp/second is:
- NEET (UG) - 2025
- Electromagnetic Induction and Inductance
- A ball of mass 0.5 kg is dropped from a height of 10 m. The ball hits the ground and rises to a height of 1.5 m. The impulse imparted to the ball during its collision with the ground is : (Take \(g = 9.8 \, \text{m/s}^2\))
- NEET (UG) - 2025
- Collision and Impulse
Concepts Used:
Law of Chemical Equilibrium
Law of Chemical Equilibrium states that at a constant temperature, the rate of a chemical reaction is directly proportional to the product of the molar concentrations of the reactants each raised to a power equal to the corresponding stoichiometric coefficients as represented by the balanced chemical equation.
Let us consider a general reversible reaction;
A+B ↔ C+D
After some time, there is a reduction in reactants A and B and an accumulation of the products C and D. As a result, the rate of the forward reaction decreases and that of backward reaction increases.
Eventually, the two reactions occur at the same rate and a state of equilibrium is attained.
By applying the Law of Mass Action;
The rate of forward reaction;
Rf = Kf [A]a [B]b
The rate of backward reaction;
Rb = Kb [C]c [D]d
Where,
[A], [B], [C] and [D] are the concentrations of A, B, C and D at equilibrium respectively.
a, b, c, and d are the stoichiometric coefficients of A, B, C and D respectively.
Kf and Kb are the rate constants of forward and backward reactions.
However, at equilibrium,
Rate of forward reaction = Rate of backward reaction.
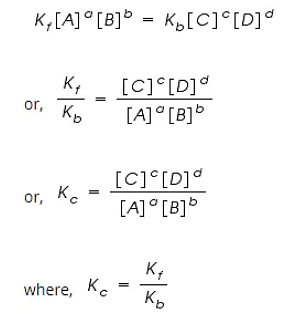
Kc is called the equilibrium constant expressed in terms of molar concentrations.
The above equation is known as the equation of Law of Chemical Equilibrium.