Question:
In the given figure, AB is the chord of the circle with centre ‘O’. A tangent AT is drawn at point ‘A’ so that angle BAT = 48°, then measure of angle ADB is :
In the given figure, AB is the chord of the circle with centre ‘O’. A tangent AT is drawn at point ‘A’ so that angle BAT = 48°, then measure of angle ADB is :
Updated On: Sep 10, 2024
- 112°
- 148°
- 132°
- 142°
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
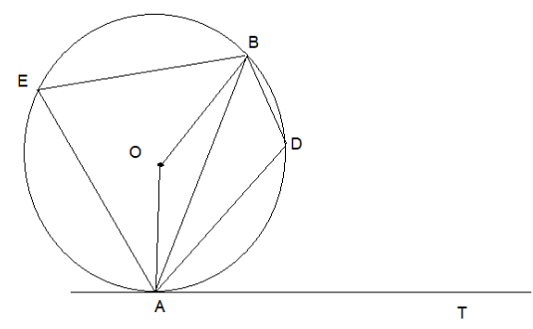
OA = OB {radii}
And angle OAT = 90° {Since, AT is tangent}
And angle OAB = 90 - 48 = 42°
In triangle OAB;
Angle OAB = angle OBA {angles opposite to equal sides are equal}
So, angle AOB = 180 - 42 - 42 = 96°
So, angle AEB = 96/2 = 48° {Since, ‘O’ is the circum-centre}
Since, AEBD is a cyclic quadrilateral.
So, angle AEB + angle ADB = 180°
Or, angle ADB = 180 - 48 = 132°
So, the correct option is (C) : 132°.
Was this answer helpful?
0
0
Top Questions on Geometry
- Consider a right-angled triangle ABC, right angled at B. Two circles, each of radius r, are drawn inside the triangle in such a way that one of them touches AB and BC, while the other one touches AC and BC. The two circles also touch each other (see the image below).
If AB = 18 cm and BC = 24 cm, then find the value of r.
- A group of boys is practising football in a rectangular ground. Raju and Ratan are standing at the two opposite mid-points of the two shorter sides. Raju has the ball, who passes it to Rivu, who is standing somewhere on one of the longer sides. Rivu holds the ball for 3 seconds and passes it to Ratan. Ratan holds the ball for 2 seconds and passes it back to Raju. The path of the ball from Raju to Rivu makes a right angle with the path of the ball from Rivu to Ratan. The speed of the ball, whenever passed, is always 10 metre per second, and the ball always moves on straight lines along the ground.
Consider the following two additional pieces of information:
I. The dimension of the ground is 80 metres × 50 metres.
II. The area of the triangle formed by Raju, Rivu and Ratan is 1000 square metres.
Consider the problem of computing the following: how many seconds does it take for Raju to get the ball back since he passed it to Rivu? Choose the correct option. - A farmer has a triangular plot of land. One side of the plot, henceforth called the base, is 300 feet long and the other two sides are equal. The perpendicular distance, from the corner of the plot, where the two equal sides meet, to the base, is 200 feet.
To counter the adverse effect of climate change, the farmer wants to dig a circular pond. He plans that half of the circular area will be inside the triangular plot and the other half will be outside, which he will purchase at the market rate from his neighbour. The diameter of the circular plot is entirely contained in the base and the circumference of the pond touches the two equal sides of the triangle from inside.
If the market rate per square feet of land is Rs. 1400, how much does the farmer must pay to buy the land from his neighbour for the pond? (Choose the closest option.) - A rectangle \(ABCD\) has sides \(AB = 45 \, \text{cm}\) and \(BC = 26 \, \text{cm}\). Point \(E\) is the midpoint of side \(CD\). Find the radius of the incircle of the triangle \(\triangle AED\).
- PQR is a triangle. The bisectors of the internal angle ∠Q and external angle ∠R intersect at M. If ∠QMR = 40°, then ∠P is:
View More Questions
Questions Asked in CAT exam
- The sum of all real values of $k$ for which $(\frac{1}{8})^k \times (\frac{1}{32768})^{\frac{4}{3}} = \frac{1}{8} \times (\frac{1}{32768})^{\frac{k}{3}}$ is
- CAT - 2024
- Logarithms
- Amal and Vimal together can complete a task in 150 days, while Vimal and Sunil together can complete the same task in 100 days. Amal starts working on the task and works for 75 days, then Vimal takes over and works for 135 days. Finally, Sunil takes over and completes the remaining task in 45 days. If Amal had started the task alone and worked on all days, Vimal had worked on every second day, and Sunil had worked on every third day, then the number of days required to complete the task would have been
- CAT - 2024
- Time and Work
- Gopi marks a price on a product in order to make 20% profit. Ravi gets 10% discount on this marked price, and thus saves Rs 15. Then, the profit, in rupees, made by Gopi by selling the product to Ravi, is
- CAT - 2024
- Profit and Loss
- Sam can complete a job in 20 days when working alone. Mohit is twice as fast as Sam and thrice as fast as Ayana in the same job. They undertake a job with an arrangement where Sam and Mohit work together on the first day, Sam and Ayana on the second day, Mohit and Ayana on the third day, and this three-day pattern is repeated till the work gets completed. Then, the fraction of total work done by Sam is
- CAT - 2024
- Time and Work
- The number of all positive integers up to 500 with non-repeating digits is
- CAT - 2024
- Number Systems
View More Questions