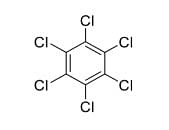
In the following reaction sequence, the major product Q is
\(\text{L-Glucose}\xrightarrow[ii)Cr_2,775K,10-20 \text{atm}]{i)HI, \Delta}P\xrightarrow[UV]{Cl_2(excess)}Q\)
\(\text{L-Glucose}\xrightarrow[ii)Cr_2,775K,10-20 \text{atm}]{i)HI, \Delta}P\xrightarrow[UV]{Cl_2(excess)}Q\)
The Correct Option is D
Solution and Explanation
To solve the problem, we analyze the reaction sequence starting from L-glucose to find the major product Q.
1. Step i) Reaction with HI and heat (\(\Delta\)):
- The sugar undergoes cleavage of C-O bonds by HI.
- This reduces glucose to a mixture of iodoalkanes (polyiodo compounds).
- The carbon skeleton remains but oxygen atoms are replaced by iodine.
2. Step ii) Oxidation with Cr\(_2\)O\(_3\), high temperature and pressure:
- Iodoalkanes are oxidized to form fully chlorinated cyclic hydrocarbons (via halogen exchange).
- Oxygen atoms are removed, and the carbon framework becomes a chlorinated cyclic structure.
3. Step iii) Treatment with excess Cl\(_2\) under UV:
- Further chlorination occurs, leading to a hexachlorinated cyclohexane derivative.
4. Structure of the final product Q:
- Hexachlorocyclohexane (all positions chlorinated).
- This corresponds to structure (D).
Final Answer:
Option (D)
Top Questions on Aldehydes, Ketones and Carboxylic Acids
- Would you expect benzaldehyde to be more reactive or less reactive in nucleophilic addition reactions than propanal? Justify your answer.
- CBSE CLASS XII - 2025
- Chemistry
- Aldehydes, Ketones and Carboxylic Acids
- The acid formed when propyl magnesium bromide is treated with CO$_2$ followed by acid hydrolysis is:
- CBSE CLASS XII - 2025
- Chemistry
- Aldehydes, Ketones and Carboxylic Acids
Convert Ethanal to But-2-enal
- CBSE CLASS XII - 2025
- Chemistry
- Aldehydes, Ketones and Carboxylic Acids
- Which of the following reagents is used in Rosenmund reduction?
- MHT CET - 2025
- Chemistry
- Aldehydes, Ketones and Carboxylic Acids
- The product obtained on the reaction of propanone with \( CH_3MgBr \) followed by hydrolysis is
- KEAM - 2025
- Chemistry
- Aldehydes, Ketones and Carboxylic Acids
Questions Asked in JEE Advanced exam
- Let a complex number \(z\) satisfy the equation: \[ |z - z_1| = 2 |z - z_2|,\quad \text{where } z_1 = 1 + 2i,\ z_2 = 3i \] Then choose the correct options:
- JEE Advanced - 2025
- complex numbers
A solid glass sphere of refractive index $ n = \sqrt{3} $ and radius $ R $ contains a spherical air cavity of radius $ \dfrac{R}{2} $, as shown in the figure. A very thin glass layer is present at the point $ O $ so that the air cavity (refractive index $ n = 1 $) remains inside the glass sphere. An unpolarized, unidirectional and monochromatic light source $ S $ emits a light ray from a point inside the glass sphere towards the periphery of the glass sphere. If the light is reflected from the point $ O $ and is fully polarized, then the angle of incidence at the inner surface of the glass sphere is $ \theta $. The value of $ \sin \theta $ is ____
- JEE Advanced - 2025
- Ray optics and optical instruments
The center of a disk of radius $ r $ and mass $ m $ is attached to a spring of spring constant $ k $, inside a ring of radius $ R>r $ as shown in the figure. The other end of the spring is attached on the periphery of the ring. Both the ring and the disk are in the same vertical plane. The disk can only roll along the inside periphery of the ring, without slipping. The spring can only be stretched or compressed along the periphery of the ring, following Hooke’s law. In equilibrium, the disk is at the bottom of the ring. Assuming small displacement of the disc, the time period of oscillation of center of mass of the disk is written as $ T = \frac{2\pi}{\omega} $. The correct expression for $ \omega $ is ( $ g $ is the acceleration due to gravity):
- JEE Advanced - 2025
- Oscillations
In a scattering experiment, a particle of mass $ 2m $ collides with another particle of mass $ m $, which is initially at rest. Assuming the collision to be perfectly elastic, the maximum angular deviation $ \theta $ of the heavier particle, as shown in the figure, in radians is:
- JEE Advanced - 2025
- Elastic and inelastic collisions
A conducting square loop initially lies in the $ XZ $ plane with its lower edge hinged along the $ X $-axis. Only in the region $ y \geq 0 $, there is a time dependent magnetic field pointing along the $ Z $-direction, $ \vec{B}(t) = B_0 (\cos \omega t) \hat{k} $, where $ B_0 $ is a constant. The magnetic field is zero everywhere else. At time $ t = 0 $, the loop starts rotating with constant angular speed $ \omega $ about the $ X $ axis in the clockwise direction as viewed from the $ +X $ axis (as shown in the figure). Ignoring self-inductance of the loop and gravity, which of the following plots correctly represents the induced e.m.f. ($ V $) in the loop as a function of time:
- JEE Advanced - 2025
- Electromagnetic induction