Question

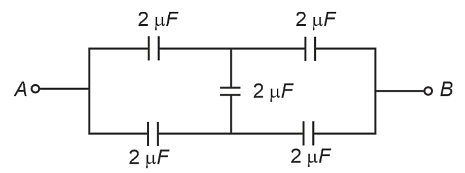
In the following circuit, the equivalent capacitance between terminal A and terminal B is :

• A. 2 µF
• B. 1 µF
• C. 0.5 µF
• D. 4 µF

Answer 1

The Correct Option is A

Step 1: Identify Capacitors in Parallel 

The given circuit consists of capacitors arranged in both series and parallel configurations.

First, observe the two 2 µF capacitors in parallel between terminal A and the intermediate node.

The formula for the equivalent capacitance of two capacitors in parallel is:

$$ C_{\text{eq, parallel}} = C_1 + C_2 $$

For the two 2 µF capacitors:

$$ C_{\text{eq, parallel}} = 2\text{ µF} + 2\text{ µF} = 4\text{ µF} $$

Step 2: Identify Capacitors in Series

Now, the 4 µF equivalent capacitance is in series with the 2 µF capacitor in the middle of the circuit.

The formula for the equivalent capacitance of capacitors in series is:

$$ \frac{1}{C_{\text{eq, series}}} = \frac{1}{C_1} + \frac{1}{C_2} $$

For the 4 µF and 2 µF capacitors in series:

$$ \frac{1}{C_{\text{eq, series}}} = \frac{1}{4} + \frac{1}{2} $$

Rewriting with a common denominator:

$$ \frac{1}{C_{\text{eq, series}}} = \frac{1}{4} + \frac{2}{4} = \frac{3}{4} $$

Thus:

$$ C_{\text{eq, series}} = \frac{4}{3} \text{ µF} $$

Step 3: Final Parallel Combination

Finally, this \(\frac{4}{3}\) µF equivalent capacitor is in parallel with the last 2 µF capacitor.

The equivalent capacitance of two capacitors in parallel is:

$$ C_{\text{eq, final}} = C_{\text{eq, series}} + C_3 $$

Substituting values:

$$ C_{\text{eq, final}} = \frac{4}{3} \text{ µF} + 2 \text{ µF} $$

Rewriting with a common denominator:

$$ C_{\text{eq, final}} = \frac{4}{3} + \frac{6}{3} = \frac{10}{3} \text{ µF} $$

Conclusion

The total equivalent capacitance between terminals A and B is:

$$ C_{\text{total}} = \frac{10}{3} \text{ µF} $$