Question

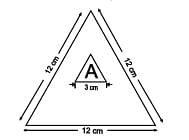
In a shooting competition, all the shooters should hit the letter space in which letter 'A' is written as shown on the target board below. What is the probability that the shooter will hit that space?

• A. \(\frac{1}{16}\)
• B. \(\frac{1}{12}\)
• C. \(\frac{1}{8}\)
• D. \(\frac{1}{4}\)
• E. \(\frac{3}{4}\)

Answer 1

The Correct Option is A

To determine the probability of hitting the space where the letter 'A' is on the target board, we need to consider the areas involved. 

From the given image, we can see a large equilateral triangle with a smaller equilateral triangle inside it. We need to find the probability of hitting the smaller triangle containing 'A'.

1. The side of the larger equilateral triangle is \(12 \, \text{cm}\), and the side of the smaller triangle is \(3 \, \text{cm}\).
2. The area of an equilateral triangle with side \(s\) is given by the formula: \(Area = \frac{\sqrt{3}}{4} s^2\).
3. Calculate the area of the larger triangle:
   • \(Area_{\text{large}} = \frac{\sqrt{3}}{4} \times 12^2 = 36\sqrt{3} \, \text{cm}^2\)
4. Calculate the area of the smaller triangle:
   • \(Area_{\text{small}} = \frac{\sqrt{3}}{4} \times 3^2 = \frac{9\sqrt{3}}{4} \, \text{cm}^2\)
5. The probability of hitting the area containing 'A' is the ratio of the area of the smaller triangle to the larger triangle:
   • \(Probability = \frac{Area_{\text{small}}}{Area_{\text{large}}} = \frac{\frac{9\sqrt{3}}{4}}{36\sqrt{3}} = \frac{1}{16}\)

Hence, the correct answer is \(\frac{1}{16}\).