If two distinct points Q, R lie on the line of intersection of the planes –x + 2y – z = 0 and 3x – 5y + 2z = 0 and
\(PQ = PR = \sqrt{18}\)
where the point P is (1, –2, 3), then the area of the triangle PQR is equal to
If two distinct points Q, R lie on the line of intersection of the planes –x + 2y – z = 0 and 3x – 5y + 2z = 0 and
\(PQ = PR = \sqrt{18}\)
where the point P is (1, –2, 3), then the area of the triangle PQR is equal to
\(\frac{2}{3} \sqrt{38}\)
\(\frac{4}{3}\sqrt{38}\)
\(\frac{8}{3}\sqrt{38}\)
\(\sqrt\frac{152}{3}\)
The Correct Option is B
Solution and Explanation
The correct answer is (B) : \(\frac{4}{3}\sqrt{38}\)
Line L is x = y = z
\(\stackrel{→}{PQ}.(\hat{i}+\hat{j}+\hat{k})=0\)
\(⇒ (α – 3) + α + 2 + α – 1 = 0\)
\(⇒ α = \frac{2}{3}\)
so,
\(T = ( \frac{2}{3}, \frac{2}{3}, \frac{2}{3})\)
\(PT = \sqrt\frac{38}{3}\)
\(⇒ QT = \frac{4}{\sqrt3}\)
So, Area
\(= ( \frac{1}{2} × \frac{4}{\sqrt3} × \frac{\sqrt{38}}{\sqrt3} ) . 2\)
\(= \frac{4\sqrt{38}}{3} sq ∼ units\)
Top Questions on Three Dimensional Geometry
- If the distances of the point \( (1,2,a) \) from the line \[ \frac{x-1}{1}=\frac{y}{2}=\frac{z-1}{1} \] along the lines \[ L_1:\ \frac{x-1}{3}=\frac{y-2}{4}=\frac{z-a}{b} \quad \text{and} \quad L_2:\ \frac{x-1}{1}=\frac{y-2}{4}=\frac{z-a}{c} \] are equal, then \( a+b+c \) is equal to:
- JEE Main - 2026
- Mathematics
- Three Dimensional Geometry
- The value of the integral \( \int_{\frac{\pi}{24}}^{\frac{5\pi}{24}} \frac{dx}{1 + \sqrt[3]{\tan 2x}} \) is :
- JEE Main - 2026
- Mathematics
- Three Dimensional Geometry
Let the lines $L_1 : \vec r = \hat i + 2\hat j + 3\hat k + \lambda(2\hat i + 3\hat j + 4\hat k)$, $\lambda \in \mathbb{R}$ and $L_2 : \vec r = (4\hat i + \hat j) + \mu(5\hat i + + 2\hat j + \hat k)$, $\mu \in \mathbb{R}$ intersect at the point $R$. Let $P$ and $Q$ be the points lying on lines $L_1$ and $L_2$, respectively, such that $|PR|=\sqrt{29}$ and $|PQ|=\sqrt{\frac{47}{3}}$. If the point $P$ lies in the first octant, then $27(QR)^2$ is equal to}
- JEE Main - 2026
- Mathematics
- Three Dimensional Geometry
- Let a line $L$ passing through the point $P(1,1,1)$ be perpendicular to the lines \[ \frac{x-4}{4}=\frac{y-1}{1}=\frac{z-1}{1} \quad \text{and} \quad \frac{x-17}{1}=\frac{y-71}{1}=\frac{z}{0}. \] Let the line $L$ intersect the $yz$-plane at the point $Q$.
Another line parallel to $L$ and passing through the point $S(1,0,-1)$ intersects the $yz$-plane at the point $R$.
Then the square of the area of the parallelogram $PQRS$ is equal to
- JEE Main - 2026
- Mathematics
- Three Dimensional Geometry
- Let \( L \) be the line \[ \frac{x+1}{2} = \frac{y+1}{3} = \frac{z+3}{6} \] and let \( S \) be the set of all points \( (a,b,c) \) on \( L \), whose distance from the line \[ \frac{x+1}{2} = \frac{y+1}{3} = \frac{z-9}{0} \] along the line \( L \) is \( 7 \). Then \[ \sum_{(a,b,c)\in S} (a+b+c) \] is equal to
- JEE Main - 2026
- Mathematics
- Three Dimensional Geometry
Questions Asked in JEE Main exam
Which one of the following graphs accurately represents the plot of partial pressure of CS₂ vs its mole fraction in a mixture of acetone and CS₂ at constant temperature?
- JEE Main - 2026
- Organic Chemistry
- For two identical cells each having emf \(E\) and internal resistance \(r\), the current through an external resistor of \(6\,\Omega\) is the same when the cells are connected in series as well as in parallel. The value of the internal resistance \(r\) is ________ \(\Omega\).
- JEE Main - 2026
- Current electricity
- For three unit vectors \( \vec a, \vec b, \vec c \) satisfying \[ |\vec a-\vec b|^2 + |\vec b-\vec c|^2 + |\vec c-\vec a|^2 = 9 \] and \[ |2\vec a + k\vec b + k\vec c| = 3, \] the positive value of \( k \) is:
- JEE Main - 2026
- Vector Algebra
In the given figure, the blocks $A$, $B$ and $C$ weigh $4\,\text{kg}$, $6\,\text{kg}$ and $8\,\text{kg}$ respectively. The coefficient of sliding friction between any two surfaces is $0.5$. The force $\vec{F}$ required to slide the block $C$ with constant speed is ___ N.
(Given: $g = 10\,\text{m s}^{-2}$)
- JEE Main - 2026
- Rotational Mechanics
- The system of linear equations
$x + y + z = 6$
$2x + 5y + az = 36$
$x + 2y + 3z = b$
has- JEE Main - 2026
- Matrices and Determinants
Concepts Used:
Three Dimensional Geometry
Mathematically, Geometry is one of the most important topics. The concepts of Geometry are derived w.r.t. the planes. So, Geometry is divided into three major categories based on its dimensions which are one-dimensional geometry, two-dimensional geometry, and three-dimensional geometry.
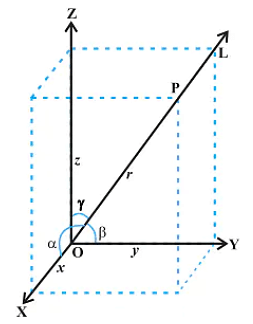
Direction Cosines and Direction Ratios of Line:
Consider a line L that is passing through the three-dimensional plane. Now, x,y and z are the axes of the plane and α,β, and γ are the three angles the line makes with these axes. These are commonly known as the direction angles of the plane. So, appropriately, we can say that cosα, cosβ, and cosγ are the direction cosines of the given line L.
