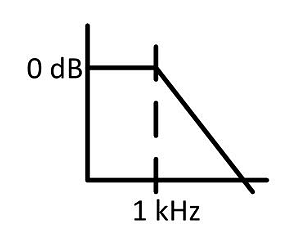
For the given Bode magnitude plot of the transfer function, the value of R is \(\underline{\hspace{2cm}}\) Ω. (Round to 2 decimals).

For the given Bode magnitude plot of the transfer function, the value of R is \(\underline{\hspace{2cm}}\) Ω. (Round to 2 decimals).

Show Hint
Correct Answer: 0.09
Solution and Explanation
Top Questions on Bode Plot
- In a bode magnitude plot, which one of the following slopes would be exhibited at high frequencies by a 4th order all-pole system?
- In a bode magnitude plot, which one of the following slopes would be exhibited at high frequencies by a 4th order all-pole system?
- The Bode plot of a 2nd order low pass filter is shown in the figure below. What is the frequency at which the attenuation is 80 dB ?
- The magnitude and phase plots of an LTI system are shown in the figure. The transfer function of the system is: \begin{center} \includegraphics[width=0.45\textwidth]{15.jpeg} \end{center}
- The Bode magnitude plot of a first order stable system is constant with frequency. The asymptotic value of the high frequency phase, for the system, is -180°. This system has

Questions Asked in GATE EE exam
A continuous time periodic signal \( x(t) \) is given by: \[ x(t) = 1 + 2\cos(2\pi t) + 2\cos(4\pi t) + 2\cos(6\pi t) \] If \( T \) is the period of \( x(t) \), then evaluate: \[ \frac{1}{T} \int_0^T |x(t)|^2 \, dt \quad {(round off to the nearest integer).} \]
- GATE EE - 2025
- Digital Signal Processing
The maximum percentage error in the equivalent resistance of two parallel connected resistors of 100 \( \Omega \) and 900 \( \Omega \), with each having a maximum 5% error, is: \[ {(round off to nearest integer value).} \]
- GATE EE - 2025
- Electrical Energy, Power
Consider a distribution feeder, with \( R/X \) ratio of 5. At the receiving end, a 350 kVA load is connected. The maximum voltage drop will occur from the sending end to the receiving end, when the power factor of the load is: \[ {(round off to three decimal places).} \]
In the circuit with ideal devices, the power MOSFET is operated with a duty cycle of 0.4 in a switching cycle with \( I = 10 \, {A} \) and \( V = 15 \, {V} \). The power delivered by the current source, in W, is: \[ {(round off to the nearest integer).} \]

- GATE EE - 2025
- Electrical Circuits
The induced emf in a 3.3 kV, 4-pole, 3-phase star-connected synchronous motor is considered to be equal and in phase with the terminal voltage under no-load condition. On application of a mechanical load, the induced emf phasor is deflected by an angle of \( 2^\circ \) mechanical with respect to the terminal voltage phasor. If the synchronous reactance is \( 2 \, \Omega \), and stator resistance is negligible, then the motor armature current magnitude, in amperes, during loaded condition is closest to: \[ {(round off to two decimal places).} \]
- GATE EE - 2025
- Electrical Energy, Power