Question:
Find the missing number from the given alternative
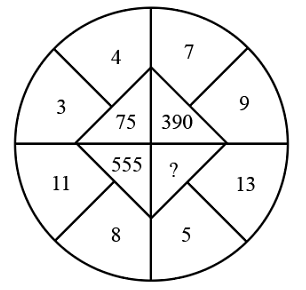
Find the missing number from the given alternative
Updated On: Dec 13, 2024
- 194
- 324
- 582
- 525
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
The correct option is(C): 582
Was this answer helpful?
3
3
Top Questions on Counting Figures
- How many squares and triangles are there in the following figure?
- TS LAWCET - 2024
- Logical Reasoning
- Counting Figures
How many straight lines are there in this figure?
- TS LAWCET - 2024
- Logical Reasoning
- Counting Figures
- How many cubes are there in a group?
- CUET (UG) - 2023
- Logical Reasoning
- Counting Figures
- Which one from the four answer figures should come at the right of the problem figures to complete the series logically?
- CUET (PG) - 2023
- Logical Reasoning
- Counting Figures
- Count the member of triangles in the following figure.
- CMAT - 2023
- Logical Reasoning
- Counting Figures
View More Questions
Questions Asked in CMAT exam
- A "Febian Entrepreneur" is a term used to describe a type of entrepreneur who focuses on gradual and steady growth rather than rapid scaling. Which of the following best describes the approach of a Febian Entrepreneur?
- CMAT - 2025
- Current Affairs
- A clock is set at 8 am. It loses 10 minutes every 24 hours. What will be the true time when the clock shows 11 am?
- CMAT - 2025
- Logical and Analytical Reasoning Skills
- The ratio of the ages of A and B is 3:5. If the sum of their ages is 48 years, what is the age of B?
- CMAT - 2025
- Current Affairs
- The first CDS (Chief of Defence Staff) of India was appointed to enhance coordination and integration among the three branches of the Indian Armed Forces. Who was the first CDS of India?
- CMAT - 2025
- Current Affairs
- Complete the series: \[ 7, 27, 107, 427, \, ? \]
- CMAT - 2025
- Logical and Analytical Reasoning Skills
View More Questions