Question:
Choose the Correct statement for the given figure:
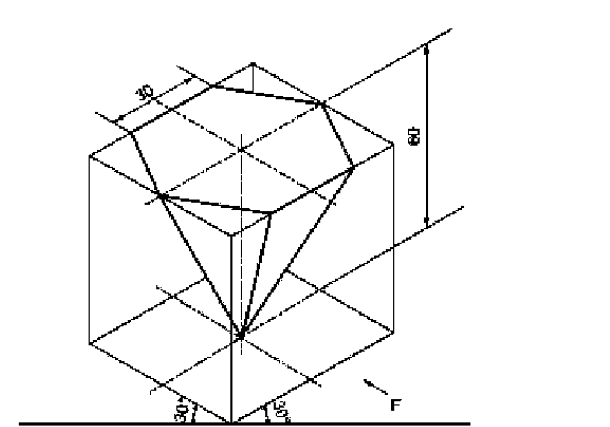
Choose the Correct statement for the given figure:
Updated On: Sep 18, 2024
- Two of its base edges are perpendicular to V.P.
- All of its base edges are parallel to V.P.
- Two of its base edges parallel to V.P.
- Its One base edge is parallel to V.P. and one base edge is perpendicular to V.P.
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
The correct option is (C):Two of its base edges parallel to V.P.
Was this answer helpful?
0
0
Top Questions on Parallel Lines
- If the line through \( (3, y) \) and \( (2, 7) \) is parallel to the line through \( (-1, 4) \) and \( (0, 6) \), then the value of \( y \) is:
- CUET (PG) - 2025
- Computer Science
- Parallel Lines
- What is the parallel line?
- UP Board X - 2025
- Chitrakala
- Parallel Lines
- The equation of a line passing through the origin and parallel to the line \[ \vec{r} = 3\hat{i} + 4\hat{j} - 5\hat{k} + t(2\hat{i} - \hat{j} + 7\hat{k}), \] where $t$ is a parameter, is:
(A) $\frac{x}{2} = \frac{y}{-1} = \frac{z}{7}$ (B) $\vec{r} = m(12\hat{i} - 6\hat{j} + 42\hat{k});$ where $m$ is the parameter (C) $\vec{r} = (12\hat{i} - 6\hat{j} + 42\hat{k}) + s(0\hat{i} - 0\hat{j} + 0\hat{k});$ where $s$ is the parameter (D) $\frac{x - 3}{3} = \frac{y - 4}{-4} = \frac{z + 5}{0}$ (E) $\frac{x}{3} = \frac{y}{4} = \frac{z}{5}$
Choose the correct answer from the options given below:- CUET (UG) - 2024
- Mathematics
- Parallel Lines
In the given figure, the value of \( \angle DEC \) is:
- JEECUP - 2024
- Mathematics
- Parallel Lines
- A line l intersects the sides PQ and PR of a \(\triangle\) PQR at L and M respectively such that LM || QR. If PL = 5·7 cm, PQ = 15·2 cm and MR = 5·5 cm, then the length of PM (in cm) is :
- CBSE Class X - 2024
- Mathematics
- Parallel Lines
View More Questions
Questions Asked in CUET exam
- Find the ratio of de-Broglie wavelengths of deuteron having energy E and \(\alpha\)-particle having energy 2E :
- CUET (UG) - 2026
- Dual nature of radiation and matter
- The de-Broglie wavelength associated with a ball of mass 150 g traveling at 30.0 m/s would be
- CUET (UG) - 2025
- de broglie hypothesis
- A clock shows the time as 3:15. What is the angle between the hour and minute hands?
- CUET (UG) - 2025
- Clock and Calendar
- If 36: 84 :: 42: X, then the value of X, is:
- CUET (UG) - 2025
- Ratio and Proportion
- The angles of elevation of the top of a tower from two points at a distance of 5 meters and 20 meters along the same straight line from the base of the tower, are complementary. Find the height of the tower.
- CUET (UG) - 2025
- Trigonometry
View More Questions