An object 5.0 cm in length is placed at a distance of 20 cm in front of a convex mirror of radius of curvature 30 cm. Find the position of the image, its nature and size.
Solution and Explanation
Object distance, \(u = −20\ cm \)
Object height, \(h = 5\ cm\)
Radius of curvature, \(R = 30\ cm \)
Radius of curvature \(= 2 × \text {Focal length}\)
\(R = 2f \)
\(f = 15\ cm \)
According to the mirror formula,
\(\frac 1v+\frac 1u=\frac 1f\)
\(\frac 1v=\frac 1f-\frac 1u\)
\(\frac 1v=\frac {1}{15}+\frac {1}{20}\)
\(\frac 1v=\frac {4+3}{60}\)
\(\frac 1v=\frac {7}{60}\)
\(v= 8.57\)
The positive value of v indicates that the image is formed behind the mirror.
Magnfication, \(m=-\frac {\text {Image\ distance}}{\text{Object\ distance}}\)
\(m =-\frac {8.57}{-20}\)
\(m=0.428\)
The positive value of magnification indicates that the image is formed is virtual.
Magnfication, \(m=-\frac {\text {Height \ of the \ Image}}{\text{Height \ of the \ Object}}\)
\(m = \frac {h'}{h}\)
\(h'=m \times h\)
\(h' =0.428 \times 5\)
\(h'=2.14\ cm\)
The positive value of image height indicates that the image formed is erect.
Therefore, the image formed is virtual, erect, and smaller in size.
Top Questions on Spherical Mirrors
- A concave mirror produces an image of an object such that the distance between the object and image is 20 cm. If the magnification of the image is \( -3 \), then the magnitude of the radius of curvature of the mirror is:
- JEE Main - 2025
- Physics
- Spherical Mirrors
- (ii) An object at a distance of 16 cm from a spherical mirror forms a virtual image at a distance of 12 cm behind the mirror. Determine the magnification of the image and type of the mirror.
- UP Board X - 2025
- Science
- Spherical Mirrors
- Image of an object formed by a concave mirror is real and of the size of the object. The object is placed -
- UP Board X - 2025
- Science
- Spherical Mirrors
- With the help of a suitable ray diagram, derive the formula \( \frac{1}{v} + \frac{1}{u} = \frac{1}{f} \) for a concave mirror.
- UP Board XII - 2025
- Physics
- Spherical Mirrors
- The length of the image formed by a concave mirror:
- UP Board XII - 2025
- Physics
- Spherical Mirrors
Questions Asked in CBSE X exam
(i) Study the diagram and name the parts marked as A, B, C, and D.
(ii) Write the function of A and C.
- CBSE Class X - 2025
- Electricity
- Matilda’s character embodies the journey of change or progression throughout the story, encapsulating the transformations she endured as a consequence of her experiences, trials, and engagements with other characters.
In the light of the above information, trace the transformation seen in Matilda’s character in the story.
(The Necklace) - Analyse the changes in Indian printing by the end of the 19th century.
- CBSE Class X - 2025
- Print Culture and the Modern World
- A box contains 120 discs, which are numbered from 1 to 120. If one disc is drawn at random from the box, find the probability that
(i) it bears a 2-digit number
(ii) the number is a perfect square.- CBSE Class X - 2025
- Probability
- What happens when butane is burnt in air? Write the chemical equation for the reaction. Differentiate between the flames obtained when butane and butyne both are burnt in air in similar conditions.
- CBSE Class X - 2025
- Chemical Reactions
Concepts Used:
Spherical Mirrors
A spherical mirror is a mirror which has been cut out of a spherical surface.
There are two kinds of spherical mirrors:
- Convex Mirror
- Concave Mirror
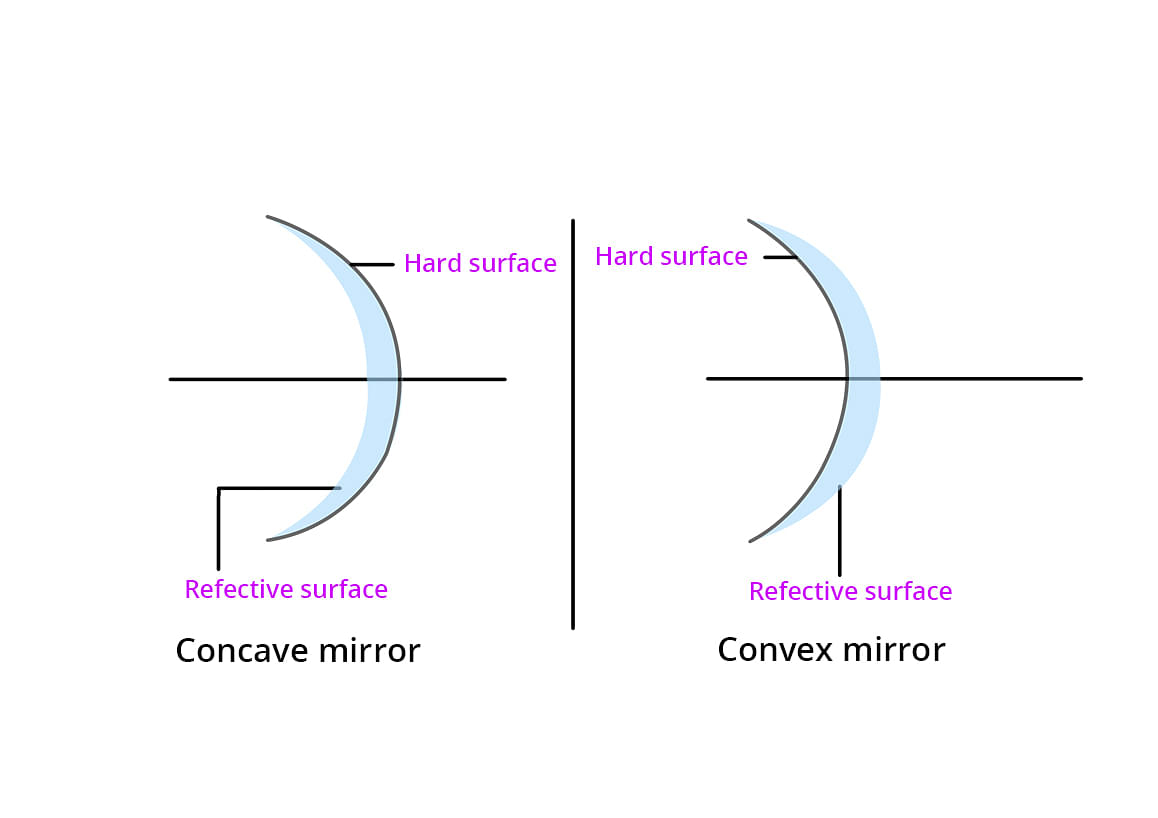
Concave Mirror
Concave mirrors are also called converging mirrors, because in these types of mirrors, light rays converge at a point after impact and reflect back from the reflective surface of the mirror.
Convex Mirror
The convex mirror has a reflective surface that is curved outward. Regardless of the distance between the subject and the mirrors, these mirrors are "always" virtual, upright and reduced.