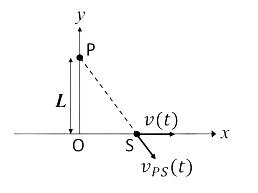
A whistle S of sound frequency f is oscillating with angular frequency 𝜔 along the x-axis. Its instantaneous position and the velocity are given by 𝑥(𝑡) = 𝑎 sin(𝜔𝑡) and 𝑣(𝑡)=𝑣0 cos (𝜔𝑡), respectively. An observer P is located on the y-axis at a distance L from the origin (see figure). Let 𝑣𝑃𝑆(𝑡) be the component of 𝑣(𝑡) along the line joining the source and the observer. Choose the correct option(s):
(Here 𝑎 and 𝑣0 are constants)
(Here 𝑎 and 𝑣0 are constants)

- 𝑣𝑃𝑆(𝑡)=\(\frac{1}{2}\frac{av_o}{\sqrt{a^2-sin^2wt+L^2}}sin(2wt)\)
- The observed frequency will be f when the source is at 𝑥 = 0 and 𝑥 = ±a
- The observed frequency will be f when the source is at position 𝑥 = ± \(\frac{a}{2}\)
- 𝑣𝑃𝑆(𝑡)=\(\frac{1}{2}\frac{av_o}{\sqrt{a^2+L^2}}sin(2wt)\)
The Correct Option is A, B
Solution and Explanation
Velocity Component Along the Line of Sight
The velocity component vPS(t) along the line joining the source and the observer is given by:
vPS(t) = v(t) cosϕ
where ϕ is the angle between the velocity vector and the line joining S and P.
Distance Between the Source and Observer
From the geometry of the problem, the distance between the source and the observer is:
r(t) = √(x(t)² + L²) = √(a² sin²(ωt) + L²)
The angle ϕ satisfies:
cosϕ = L / r(t)
Velocity Component Substitution
Substituting v(t) = v0 cos(ωt) and cosϕ = L / r(t), we have:
vPS(t) = v0 cos(ωt) × (L / √(a² sin²(ωt) + L²))
Using Trigonometric Identities
The component along the line of sight becomes:
vPS(t) = (1/2) × (a v0 / √(a² sin²(ωt) + L²)) sin(2ωt)
Thus, statement (A) is correct.
Doppler Effect and Observed Frequency
The observed frequency is given by the Doppler effect, which depends on the relative velocity component vPS(t).
- At x = 0 (midpoint of oscillation) and x = ±a (extremes of oscillation), the relative velocity component becomes zero, and the observed frequency equals the original frequency f.
Hence, statement (B) is correct.
Analyzing Other Statements
- At x = ±a/2, the velocity component vPS(t) is nonzero, so the observed frequency differs from f.
- Statement (D) is incorrect because vPS(t) depends on the varying distance r(t), not just √(a² + L²).
Conclusion
The correct statements are (A) and (B).
Top Questions on Waves and Oscillations
In an oscillating spring mass system, a spring is connected to a box filled with sand. As the box oscillates, sand leaks slowly out of the box vertically so that the average frequency ω(t) and average amplitude A(t) of the system change with time t. Which one of the following options schematically depicts these changes correctly?

- NEET (UG) - 2025
- Physics
- Waves and Oscillations
- Two identical point masses P and Q, suspended from two separate massless springs of spring constants \(k_1\) and \(k_2\), respectively, oscillate vertically. If their maximum velocities are the same, the ratio of the amplitude of P to the amplitude of Q is :
- NEET (UG) - 2025
- Physics
- Waves and Oscillations
- A particle is executing simple harmonic motion with an amplitude of 10 cm. If the kinetic energy of the particle at a distance of 6 cm from the mean position is 100 J, then the kinetic energy of the particle at a distance of 2 cm from the mean position is
- TS EAMCET - 2025
- Physics
- Waves and Oscillations
The center of a disk of radius $ r $ and mass $ m $ is attached to a spring of spring constant $ k $, inside a ring of radius $ R>r $ as shown in the figure. The other end of the spring is attached on the periphery of the ring. Both the ring and the disk are in the same vertical plane. The disk can only roll along the inside periphery of the ring, without slipping. The spring can only be stretched or compressed along the periphery of the ring, following Hooke’s law. In equilibrium, the disk is at the bottom of the ring. Assuming small displacement of the disc, the time period of oscillation of center of mass of the disk is written as $ T = \frac{2\pi}{\omega} $. The correct expression for $ \omega $ is ( $ g $ is the acceleration due to gravity):

- JEE Advanced - 2025
- Physics
- Waves and Oscillations
- Two bodies A and B of equal mass are suspended from two massless springs of spring constant \( k_1 \) and \( k_2 \), respectively. If the bodies oscillate vertically such that their amplitudes are equal, the ratio of the maximum velocity of A to the maximum velocity of B is:
- JEE Main - 2025
- Physics
- Waves and Oscillations
Questions Asked in IIT JAM exam
- Consider a volume V enclosed by a closed surface S having unit surface normal \(\hat{n}\). For \(\mathbf{r} = x\hat{i} + y\hat{j} + z\hat{k}\), the value of the surface integral \(\frac{1}{9} \oint_{S} \mathbf{r} \cdot \hat{n} \,dS\) is
- IIT JAM PH - 2025
- Vector Calculus
- For a Zener diode as shown in the circuit diagram below, the Zener voltage \(V_Z\) is 3.7 V. For a load resistance (\(R_L\)) of 1 k\(\Omega\), a current \(I_1\) flows through the load. If \(R_L\) is decreased to 500 \(\Omega\), the current changes to \(I_2\). The ratio \(\frac{I_2}{I_1}\) is \rule{1cm{0.15mm}. (up to two decimal places)}

- IIT JAM PH - 2025
- Analog Electronics
- The shortest distance between an object and its real image formed by a thin convex lens of focal length 20 cm is _____ cm. (in integer)
- If \(\left(\frac{1-i}{1+i}\right)^{n/2} = -1\), where \(i = \sqrt{-1}\), one possible value of n is
- IIT JAM PH - 2025
- Complex numbers
- In a two-level atomic system, the excited state is 0.2 eV above the ground state. Considering the Maxwell-Boltzmann distribution, the temperature at which 2% of the atoms will be in the excited state is _____ K. (up to two decimal places)
(Boltzmann constant \(k_B = 8.62 \times 10^{-5}\) eV/K)
- IIT JAM PH - 2025
- Mechanics