Question:
A thermodynamic system is taken through the cycle abcda. The work done by the gas along the path bc is :
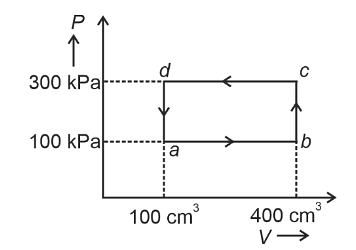
A thermodynamic system is taken through the cycle abcda. The work done by the gas along the path bc is :


Updated On: May 3, 2025
- Zero
- 30 J
- –90 J
- –60 J
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
Understanding the Concept
Work done by a gas in a thermodynamic process is given by the integral of pressure with respect to volume:
\[ W = \int P \, dV \]
In simpler terms, on a P-V diagram, the work done is represented by the area under the curve for the given process.
Analyzing Path bc
Looking at the P-V diagram, path bc is a vertical line. This means the volume remains constant during this process. Such a process is called an isochoric or isovolumetric process.
Since the volume doesn't change (dV = 0), the work done along this path is:
\[ W = \int P \, dV = 0 \]
Therefore, the work done by the gas along the path bc is 0.
Was this answer helpful?
3
3
Top Questions on Thermodynamics
- Determine the final temperature when two bodies at different temperatures are brought into thermal contact.
- BITSAT - 2025
- Physics
- Thermodynamics
- How much heat is required to raise the temperature of \( 2 \, \text{kg} \) of water from \( 25^\circ C \) to \( 75^\circ C \)? (Specific heat capacity of water \( c = 4200 \, \text{J/kg}^\circ C \))
- BITSAT - 2025
- Physics
- Thermodynamics
- An ideal gas undergoes an adiabatic expansion from volume \( V \) to \( 2V \). If the initial temperature is \( T \), what is the final temperature? (Assume the ratio of specific heats \( \gamma = \frac{5}{3} \))
- BITSAT - 2025
- Physics
- Thermodynamics
- The reaction \( {A}_2 + {B}_2 \to 2{AB} \) follows the mechanism: \[ {A}_2 \xrightarrow{k_1} {A} + {A} \ ({fast}) \quad {A} + {B}_2 \xrightarrow{k_2} {AB} + {B} \ ({slow}) \quad {A} + {B} \to {AB} \ ({fast}) \] The overall order of the reaction is:
- JEE Main - 2025
- Chemistry
- Thermodynamics
- A gas is kept in a container having walls which are thermally non-conducting. Initially the gas has a volume of 800 $ cm^3 $ and temperature 27°C. The change in temperature when the gas is adiabatically compressed to 200 $ cm^3 $ is: (Take $ \gamma $ = 1.5 : $ \gamma $ is the ratio of specific heats at constant pressure and at constant volume)
- JEE Main - 2025
- Physics
- Thermodynamics
View More Questions
Questions Asked in NEET exam
- A microscope has an objective of focal length \(f_o = 2\) cm and an eyepiece of focal length \(f_e = 4\) cm. The tube length of the microscope is \(L = 40\) cm. If the distance of distinct vision of eye is \(D = 25\) cm, the magnification in the microscope is:
- NEET (UG) - 2025
- Optical Instruments
- Which one of the following is an example of ex-situ conservation?
- NEET (UG) - 2025
- Ex-Situ Conservation
- Which one of the following compounds can exist as cis-trans isomers?
- NEET (UG) - 2025
- Organic Chemistry
- Who proposed that the genetic code for amino acids should be made up of three nucleotides?
- NEET (UG) - 2025
- Molecular Biology
- An electron (mass \(9 \times 10^{-31}\) kg and charge \(1.6 \times 10^{-19}\) C) moving with speed \(c/100\) (\(c\) = speed of light) is injected into a magnetic field of magnitude \(9 \times 10^{-4}\) T perpendicular to its direction of motion. We wish to apply a uniform electric field \( \vec{E} \) together with the magnetic field so that the electron does not deflect from its path. (speed of light \(c = 3 \times 10^8\) m/s):
- NEET (UG) - 2025
- Electric Field
View More Questions