A spherical surface of radius of curvature R, separates air (refractive index 1.0) from glass (refractive index 1.5). The centre of curvature is in the glass. A point object P placed in air is found to have a real image Q in the glass. The line PQ cuts the surface at a point O and PO = O The distance PO is equal to
- 5 R
- 3 R
- 2 R
- 1.5 R
The Correct Option is A
Solution and Explanation
The correct option is(A): 5 R.
Let us say PO = OQ = X
Applying\(\, \, \, \, \, \, \, \, \frac{\mu_2}{v}-\frac{\mu_1}{u}=\frac{\mu_1-\mu_2}{R}\)
Substituting the values with sign
\(\frac{1.5}{+X}-\frac{1.0}{-X}=\frac{1.5-1.0}{+R}\)
(Distances are measured from O and are taken as positive in
the direction of ray of light)
\(\therefore\hspace15mm \frac{2.5}{X}=\frac{0.5}{R}\)
\(\therefore\hspace15mm X=5R\)
Top Questions on Spherical Mirrors
- A concave mirror produces an image of an object such that the distance between the object and image is 20 cm. If the magnification of the image is \( -3 \), then the magnitude of the radius of curvature of the mirror is:
- JEE Main - 2025
- Physics
- Spherical Mirrors
- (ii) An object at a distance of 16 cm from a spherical mirror forms a virtual image at a distance of 12 cm behind the mirror. Determine the magnification of the image and type of the mirror.
- UP Board X - 2025
- Science
- Spherical Mirrors
- Image of an object formed by a concave mirror is real and of the size of the object. The object is placed -
- UP Board X - 2025
- Science
- Spherical Mirrors
- With the help of a suitable ray diagram, derive the formula \( \frac{1}{v} + \frac{1}{u} = \frac{1}{f} \) for a concave mirror.
- UP Board XII - 2025
- Physics
- Spherical Mirrors
- The length of the image formed by a concave mirror:
- UP Board XII - 2025
- Physics
- Spherical Mirrors
Questions Asked in NEET exam
- A microscope has an objective of focal length \(f_o = 2\) cm and an eyepiece of focal length \(f_e = 4\) cm. The tube length of the microscope is \(L = 40\) cm. If the distance of distinct vision of eye is \(D = 25\) cm, the magnification in the microscope is:
- NEET (UG) - 2025
- Optical Instruments
- Which one of the following is an example of ex-situ conservation?
- NEET (UG) - 2025
- Ex-Situ Conservation
- Which one of the following compounds can exist as cis-trans isomers?
- NEET (UG) - 2025
- Organic Chemistry
- Who proposed that the genetic code for amino acids should be made up of three nucleotides?
- NEET (UG) - 2025
- Molecular Biology
- An electron (mass \(9 \times 10^{-31}\) kg and charge \(1.6 \times 10^{-19}\) C) moving with speed \(c/100\) (\(c\) = speed of light) is injected into a magnetic field of magnitude \(9 \times 10^{-4}\) T perpendicular to its direction of motion. We wish to apply a uniform electric field \( \vec{E} \) together with the magnetic field so that the electron does not deflect from its path. (speed of light \(c = 3 \times 10^8\) m/s):
- NEET (UG) - 2025
- Electric Field
Concepts Used:
Spherical Mirrors
A spherical mirror is a mirror which has been cut out of a spherical surface.
There are two kinds of spherical mirrors:
- Convex Mirror
- Concave Mirror
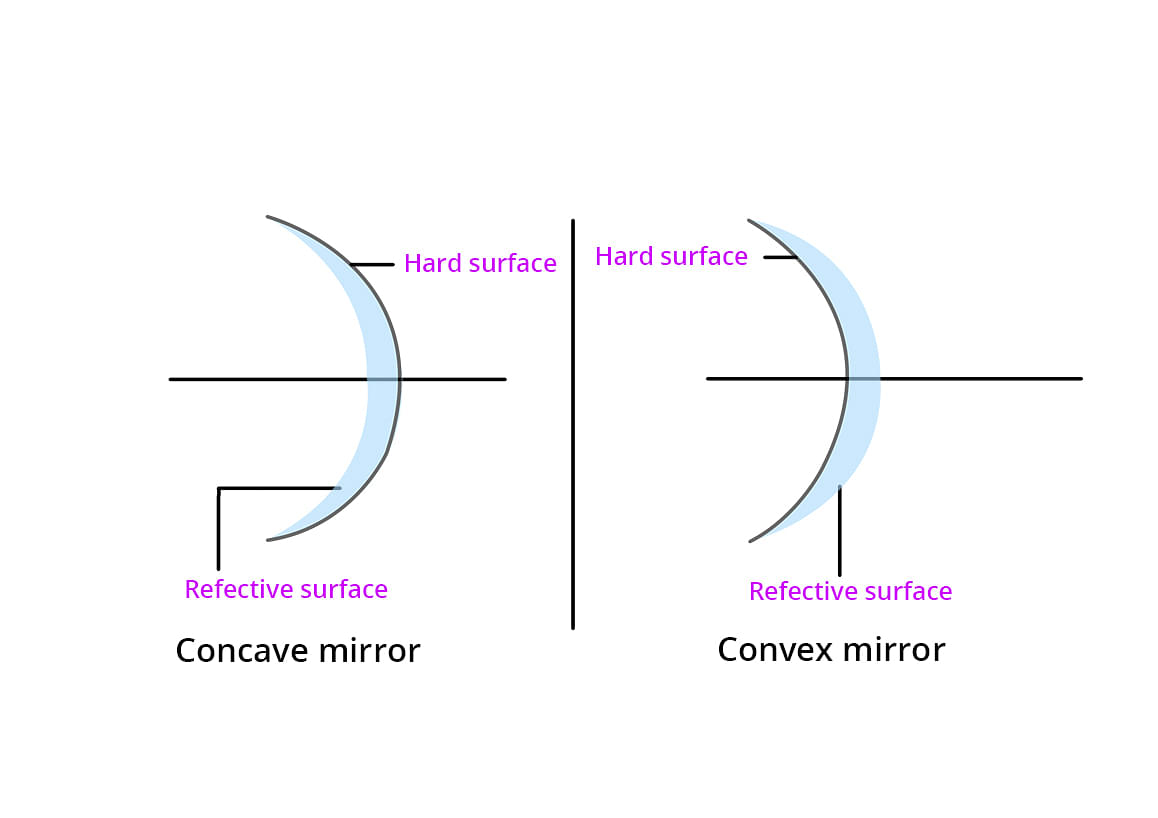
Concave Mirror
Concave mirrors are also called converging mirrors, because in these types of mirrors, light rays converge at a point after impact and reflect back from the reflective surface of the mirror.
Convex Mirror
The convex mirror has a reflective surface that is curved outward. Regardless of the distance between the subject and the mirrors, these mirrors are "always" virtual, upright and reduced.