A longitudinal pressure wave travelling inside a muscle tissue is incident at an angle of 60° at the interface between the muscle and kidney. Let the wave impedance be \( Z_{\text{muscle}} = 1.70 \times 10^5 \, \text{g cm}^{-2} \, \text{s}^{-1} \), \( Z_{\text{kidney}} = 1.62 \times 10^5 \, \text{g cm}^{-2} \, \text{s}^{-1} \) and wave velocities in muscle and kidney tissues be 1590 and 1560 m/s respectively. The transducer centre frequency is 1.5 MHz. The pressure wave propagation angle in the kidney tissue and intensity transmission coefficient at the tissue interface are \(\underline{\hspace{2cm}}\) degrees (rounded off to the nearest integer) and \(\underline{\hspace{2cm}}\) (rounded off to two decimal places), respectively.
Show Hint
- 58.0, 0.24
- 30.0, 0.68
- 58.0, 0.94
- 30.0, 0.99
The Correct Option is C
Solution and Explanation
Step 1: Calculate the angle of propagation.
Using Snell's Law for wave transmission, the relationship between the angle of propagation in the muscle and kidney tissues is given by:
\[
\frac{\sin \theta_1}{\sin \theta_2} = \frac{V_{\text{muscle}}}{V_{\text{kidney}}}
\]
Where \( \theta_1 = 60^\circ \) (angle of incidence), and \( V_{\text{muscle}} = 1590 \, \text{m/s} \), \( V_{\text{kidney}} = 1560 \, \text{m/s} \).
Solving for \( \theta_2 \), we get:
\[
\sin \theta_2 = \frac{V_{\text{kidney}}}{V_{\text{muscle}}} \sin \theta_1
\]
\[
\sin \theta_2 = \frac{1560}{1590} \sin 60^\circ = 0.980 \times 0.866 = 0.849
\]
Thus,
\[
\theta_2 = \sin^{-1}(0.849) = 58^\circ
\]
Step 2: Calculate the intensity transmission coefficient.
The intensity transmission coefficient \( T \) is given by:
\[
T = \left( \frac{2Z_{\text{muscle}}}{Z_{\text{muscle}} + Z_{\text{kidney}}} \right)^2
\]
Substituting the values:
\[
T = \left( \frac{2 \times 1.70 \times 10^5}{1.70 \times 10^5 + 1.62 \times 10^5} \right)^2 = \left( \frac{3.40 \times 10^5}{3.32 \times 10^5} \right)^2 = (1.02)^2 = 1.04
\]
Rounded off, the intensity transmission coefficient is 0.94.
Thus, the correct answers are 58.0 degrees and 0.94.
Top Questions on Ultrasound and its application
- Which of the following statement(s) about ultrasound waves is/are true?
- GATE BM - 2025
- Medical Imaging Systems
- Ultrasound and its application
- If a circular ultrasound transducer of radius a = 8 mm operating at a central frequency of 1 MHz has a pressure beam pattern in a medium as given below :
\(P(r,0) \propto\sin\frac{ka^2}{4r}\)
Here, k is the wave number, r is the axial distance from the center of aperture. The speed of sound in the medium is 1600 ms-1.
The reduction in intensity between r = 8 cm and r = 16 cm is _______ dB. Give your answer as a positive quantity rounded off to two decimal places.- GATE BM - 2024
- Medical Imaging Systems
- Ultrasound and its application
- A Doppler ultrasound transducer operating at 5 MHz gave maximum output frequency shift of 3 kHz. The velocity of sound in blood is 1500 m/s. If the probe was held at an angle of 45° to the direction of blood flow, the maximum velocity of blood flow through the artery is _______ m/s. (Give your answer rounded off to two decimal places.)
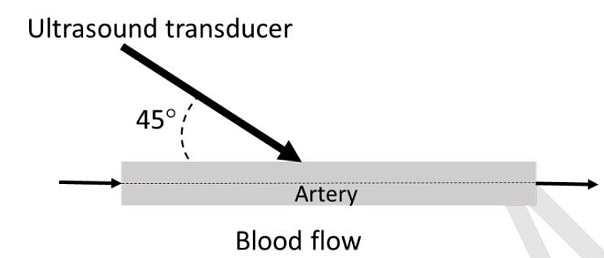
- GATE BM - 2024
- Medical Imaging Systems
- Ultrasound and its application
- The 1stgeneration (1G) CT scanner uses a point X-ray source and a detector. The source-detector assembly can move linearly at a speed of 0.5 m.s\(^{-1}\) and it takes 0.5 s for source-detector assembly to rotate one angular increment, regardless of the angle. This scanner is expected to collect 360 projections over 180° of span. The field of view used for data collection has a diameter of 0.5 m. The scan time required is _____ s.
- GATE BM - 2022
- Medical Imaging Systems
- Ultrasound and its application
- Backscattered electron detector of a scanning electron microscope is used to
- GATE BM - 2022
- Medical Imaging Systems
- Ultrasound and its application
Questions Asked in GATE BM exam
Eight students (P, Q, R, S, T, U, V, and W) are playing musical chairs. The figure indicates their order of position at the start of the game. They play the game by moving forward in a circle in the clockwise direction.
After the 1st round, the 4th student behind P leaves the game.
After the 2nd round, the 5th student behind Q leaves the game.
After the 3rd round, the 3rd student behind V leaves the game.
After the 4th round, the 4th student behind U leaves the game.
Who all are left in the game after the 4th round?
Here are two analogous groups, Group-I and Group-II, that list words in their decreasing order of intensity. Identify the missing word in Group-II.
Abuse \( \rightarrow \) Insult \( \rightarrow \) Ridicule
__________ \( \rightarrow \) Praise \( \rightarrow \) Appreciate
The following figures show three curves generated using an iterative algorithm. The total length of the curve generated after 'Iteration n' is:

- Had I learnt acting as a child, I ________ a famous film star.
Select the most appropriate option to complete the above sentence. The 12 musical notes are given as \( C, C^\#, D, D^\#, E, F, F^\#, G, G^\#, A, A^\#, B \). Frequency of each note is \( \sqrt[12]{2} \) times the frequency of the previous note. If the frequency of the note C is 130.8 Hz, then the ratio of frequencies of notes F# and C is: