Question:
A closed system consists of a solution of liquid water and ethanol in equilibrium with its vapours. Using the Gibbs phase rule, the degree of freedom of the system is:
A closed system consists of a solution of liquid water and ethanol in equilibrium with its vapours. Using the Gibbs phase rule, the degree of freedom of the system is:
Show Hint
The Gibbs phase rule helps in determining the number of independent variables (such as pressure, temperature) that can be specified in a system at equilibrium.
Updated On: Jan 6, 2026
- 0
- 1
- 2
- 3
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
The Gibbs phase rule is used to determine the degree of freedom in a system. The formula for the degree of freedom (\( F \)) is given by:
\[
F = C - P + 2,
\]
where \( C \) is the number of components and \( P \) is the number of phases. In this case:
- The system consists of two components: liquid water and ethanol.
- The system is in equilibrium with its vapours, meaning there are two phases (liquid and vapour).
Thus, the degree of freedom is: \[ F = 2 - 2 + 2 = 2. \] Hence, the correct answer is \( (C) 2 \). Final Answer: (C) 2
- The system consists of two components: liquid water and ethanol.
- The system is in equilibrium with its vapours, meaning there are two phases (liquid and vapour).
Thus, the degree of freedom is: \[ F = 2 - 2 + 2 = 2. \] Hence, the correct answer is \( (C) 2 \). Final Answer: (C) 2
Was this answer helpful?
0
0
Top Questions on Phase rule
- Let \( p(\bar{p}, \bar{q}, t) \) be the phase space density of an ensemble of a system. The Hamiltonian of the system is \( H(p, q) \). If \( \{A, B\} \) denotes the Poisson bracket of \( A \) and \( B \), then \( \frac{dp}{dt} = 0 \) implies
- GATE PH - 2024
- Electronics
- Phase rule
- The following figure shows an experimental liquid-liquid phase diagram of phenol and water at the vapor pressure of the system. The total amount of phenol and water (in mol) present in the phenol-rich phase when 5 mol of water was shaken with 5 mol of phenol at 40 °C is _______.
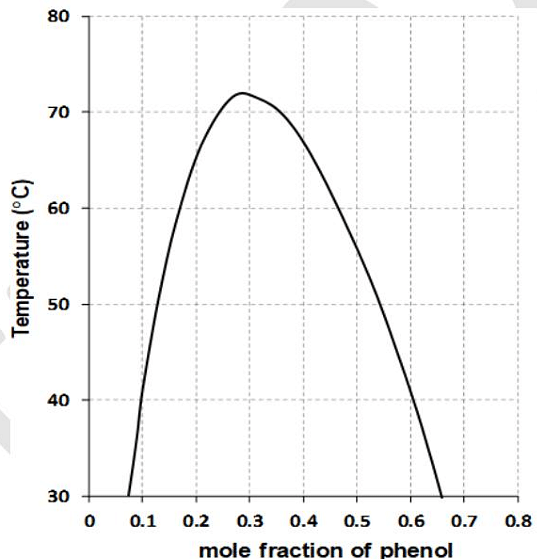
(rounded off to one decimal place) - The phase space is a
- CUET (PG) - 2023
- Physics
- Phase rule
- The Lissajous figure may be a straight line if the phase difference is
- CUET (PG) - 2023
- Physics
- Phase rule
- The correct statement(s) about actinides is/are:
Questions Asked in GATE XE exam
- Consider the infinite series
\[ (P): \sum_{n=2}^{\infty} \frac{1}{(n \log n)^{1/n}} {and} (Q): \sum_{n=1}^{\infty} \frac{n^n}{(2n)!}. \] Then which one of the following statements is correct?- GATE XE - 2025
- Sequence and Series
An electricity utility company charges ₹7 per kWh. If a 40-watt desk light is left on for 10 hours each night for 180 days, what would be the cost of energy consumption? If the desk light is on for 2 more hours each night for the 180 days, what would be the percentage-increase in the cost of energy consumption?
- The vertical (depth) profiles for three parameters P1, P2, and P3 in the northern Indian Ocean are given in the figure. The values along the x-axis are the normalized values of the parameters and the y-axis is the depth (m). Identify the parameters P1, P2, and P3 from the options given below.
- GATE XE - 2025
- Atmospheric Science
- The sea surface height concentric isolines (\(L1\) and \(L2\) in cm) and the distance between them (\(dx\) in km) for three different eddies at the same latitude are given in the figure. Which one of the following orders is correct about the magnitudes of the geostrophic currents within the isolines?
- GATE XE - 2025
- Atmospheric Science
- A rotating weather system has a tangential velocity of \(100~\mathrm{m/s}\), diameter of \(1~\mathrm{km}\), and located at a latitude where the Coriolis parameter is \(10^{-4}~\mathrm{s^{-1}}\). Which one of the following statements is true about this weather system?
- GATE XE - 2025
- Atmospheric Science
View More Questions