Question

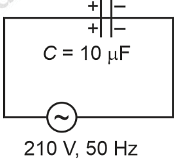
A 10 µF capacitor is connected to a 210 V, 50 Hz source as shown in figure. The peak current in the circuit is nearly (π = 3.14) :
:

• A. 0.58 A
• B. 0.93 A
• C. 1.20 A
• D. 0.35 A

Answer 1

The Correct Option is B

Capacitive Reactance

$$ X_C = \frac{1}{\omega C} = \frac{1}{2 \pi f C} $$

$$ X_C = \frac{1}{2 \times 3.14 \times 50 \times 10 \times 10^{-6}} = \frac{1000}{3.14} $$

$$ V_{rms} = 210 \ V $$

$$ i_{rms} = \frac{V_{rms}}{X_c} = \frac{210}{X_c} $$

Peak current \( = \sqrt{2} i_{rms} \)

$$ = \sqrt{2} \times \frac{210}{1000} \times 3.14 = 0.932 \simeq 0.93 \ A $$

Answer 2

Step 1: Recall the Formula for Capacitive Reactance 

The capacitive reactance is given by:

$$ X_C = \frac{1}{2\pi f C} $$

Given values:

• \( f = 50 \) Hz
• \( C = 10 \mu F = 10 \times 10^{-6} \) F

Step 2: Calculate \( X_C \)

$$ X_C = \frac{1}{2\pi (50) (10 \times 10^{-6})} $$

Solving:

$$ X_C = \frac{1}{3.14 \times 10^{-3}} $$

$$ X_C \approx 318.47 \, \Omega $$

Step 3: Calculate the Peak Current

The peak current is given by:

$$ I_0 = \frac{V_0}{X_C} $$

Where:

$$ V_0 = \sqrt{2} V_{\text{rms}} = \sqrt{2} (210) $$

$$ V_0 \approx 296.98 \text{ V} $$

Substituting values:

$$ I_0 = \frac{296.98}{318.47} $$

$$ I_0 \approx 0.93 \text{ A} $$

Step 4: Conclusion

The peak current is approximately 0.93 A.