Integrate the function: \(\frac{1}{\sqrt{x+a}+\sqrt{x+b}}\)
Solution and Explanation
\(\frac{1}{\sqrt{x+a}+\sqrt{x+b}}\)=\(\frac{1}{\sqrt{x+a}+\sqrt{x+b}}\)×\(\sqrt{x+a}\)-\(\frac{\sqrt{x+b}}{\sqrt{x+a}}\)-\(\sqrt{x+b}\)
=\(\frac{\sqrt{x+a}-\sqrt{x+b}}{(x+a)-(x+b)}\)
⇒\(\int \frac{1}{\sqrt{x+a}}=\sqrt{x}+bdx=\frac{1}{a}-b\int (\sqrt{x+a}=\sqrt{x+b})dx\)
=\(\frac{2}{3}\)(a-b)[(x+a)\(^{\frac{3}{2}}\)-(x+b)\(^{\frac{3}{2}}\)]+C
Top Questions on integral
Let \( f : (0, \infty) \to \mathbb{R} \) be a twice differentiable function. If for some \( a \neq 0 \), } \[ \int_0^a f(x) \, dx = f(a), \quad f(1) = 1, \quad f(16) = \frac{1}{8}, \quad \text{then } 16 - f^{-1}\left( \frac{1}{16} \right) \text{ is equal to:}\]
- Let $ f(x) $ be a positive function and $I_1 = \int_{-\frac{1}{2}}^1 2x \, f\left(2x(1-2x)\right) dx$ and $I_2 = \int_{-1}^2 f\left(x(1-x)\right) dx.$ Then the value of $\frac{I_2}{I_1}$ is equal to ____
- Evaluate the integral: \[ \int \frac{x^2 + 2x}{\sqrt{x^2 + 1}} \, dx \]
- Evaluate the integral: \[ \int \sqrt{x^2 + 3x} \, dx \]
- The value of the integral \( \int_0^1 x^2 \, dx \) is:
Questions Asked in CBSE CLASS XII exam

A ladder of fixed length \( h \) is to be placed along the wall such that it is free to move along the height of the wall.
Based upon the above information, answer the following questions:(iii) (b) If the foot of the ladder, whose length is 5 m, is being pulled towards the wall such that the rate of decrease of distance \( y \) is \( 2 \, \text{m/s} \), then at what rate is the height on the wall \( x \) increasing when the foot of the ladder is 3 m away from the wall?
- CBSE CLASS XII - 2025
- Application of derivatives
- A meeting will be held only if all three members A, B and C are present. The probability that member A does not turn up is 0.10, member B does not turn up is 0.20 and member C does not turn up is 0.05. The probability of the meeting being cancelled is:
- CBSE CLASS XII - 2025
- Probability
- Vishesh, Manik and Amit were partners in the ratio 5 : 4 : 1. Amit retired on 31st March, 2024. Vishesh and Manik decided to share Amit’s share in the ratio 2 : 3. What will be the new profit sharing ratio between Vishesh and Manik?
- CBSE CLASS XII - 2025
- Retirement and Death of a Partner
- The electric field in a region is given by \( \vec{E} = 40x \hat{i} \, \text{N/C}. \) Find the amount of work done in taking a unit positive charge from a point (0, 3m) to the point (5m, 0).
- CBSE CLASS XII - 2025
- Electrostatics
- Consider the Linear Programming Problem, where the objective function \[ Z = x + 4y \] needs to be minimized subject to the following constraints: \[ 2x + y \geq 1000, \] \[ x + 2y \geq 800, \] \[ x \geq 0, \quad y \geq 0. \] Draw a neat graph of the feasible region and find the minimum value of $Z$.
- CBSE CLASS XII - 2025
- Linear Programming Problem
Concepts Used:
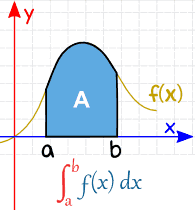
Definite Integral
Definite integral is an operation on functions which approximates the sum of the values (of the function) weighted by the length (or measure) of the intervals for which the function takes that value.
Definite integrals - Important Formulae Handbook
A real valued function being evaluated (integrated) over the closed interval [a, b] is written as :
\(\int_{a}^{b}f(x)dx\)
Definite integrals have a lot of applications. Its main application is that it is used to find out the area under the curve of a function, as shown below: