The population $p(t)$ at time $t$ of a certain mouse species satisfies the differential equation $\frac{dp\left(t\right)}{dt} = 0.5 p\left(t\right) - 450.$ If $p\left(0\right) = 850$, then the time at which the population becomes zero is :
- $2 \,\ell n \,18$
- $\ell n \,9$
- $\frac{1}{2} \,\ell n \,18$
- $\ell n \,18$
The Correct Option is A
Solution and Explanation
Top Questions on types of differential equations
- The population \( p(t) \) of a certain mouse species follows \[ \frac{dp}{dt} = 0.5p - 450. \] If \( p(0)=850 \), then the time at which population becomes zero is:}
- WBJEE JENPAS UG - 2026
- Mathematics
- types of differential equations
- If \[ x = \int_0^y \frac{1}{\sqrt{1+9t^2}} \, dt \quad \text{and} \quad \frac{d^2 y}{dx^2} = ay, \] then \( a \) is equal to:
- WBJEE JENPAS UG - 2026
- Mathematics
- types of differential equations
Consider the parabola \(25[(x-2)^2 + (y+5)^2] = (3x+4y-1)^2\), match the characteristic of this parabola given in List-I with its corresponding item in List-II.

- TS EAMCET - 2024
- Mathematics
- types of differential equations
- The axis of a parabola is parallel to Y-axis. If this parabola passes through the points \( (1,0), (0,2), (-1,-1) \) and its equation is \( ax^2 + bx + cy + d = 0 \), then \( \frac{ad}{bc} \) is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
- If the common chord of the circles \( x^2 + y^2 - 2x + 2y + 1 = 0 \) and \( x^2 + y^2 - 2x - 2y - 2 = 0 \) is the diameter of a circle \( S \), then the centre of the circle \( S \) is:
- TS EAMCET - 2024
- Mathematics
- types of differential equations
Questions Asked in AIEEE exam
- A steel wire can sustain $100\, kg$ weight without breaking. If the wire is cut into two equal parts, each part can sustain a weight of
- AIEEE - 2012
- mechanical properties of solids
- If the line $y = mx + 1$ meets the circle $x^2 + y^2 + 3x = 0 $ in two points equidistant from and on opposite sides of $x$-axis, then
- AIEEE - 2012
- Conic sections
- This question has Statement 1 and Statement 2. Of the four choices given after the Statements, choose the one that best describes the two Statements. If you push on a cart being pulled by a horse so that it does not move, the cart pushes you back with an equal and opposite force. The cart does not move because the force described in statement 1 cancel each other.
- AIEEE - 2012
- potential energy
- The variance of first n odd natural numbers is $\frac{n^{2}-1}{3}$ : The sum of first n odd natural number is $n^2$ and the sum of square of first n odd natural numbers is $\frac{n\left(4n^{2}-1\right)}{3}.$
- AIEEE - 2012
- Variance and Standard Deviation
- The ratio of number of oxygen atoms (O) in 16.0 g ozone $(O_3), \,28.0\, g$ carbon monoxide $(CO)$ and $16.0$ oxygen $(O_2)$ is (Atomic mass: $C = 12,0 = 16$ and Avogadro?? constant $N_A = 6.0 x 10^{23}\, mol^{-1}$)
- AIEEE - 2012
- Mole concept and Molar Masses
Concepts Used:
Types of Differential Equations
There are various types of Differential Equation, such as:
Ordinary Differential Equations:
Ordinary Differential Equations is an equation that indicates the relation of having one independent variable x, and one dependent variable y, along with some of its other derivatives.
\(F(\frac{dy}{dt},y,t) = 0\)
Partial Differential Equations:
A partial differential equation is a type, in which the equation carries many unknown variables with their partial derivatives.
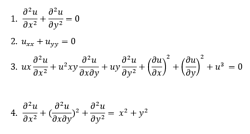
Linear Differential Equations:
It is the linear polynomial equation in which derivatives of different variables exist. Linear Partial Differential Equation derivatives are partial and function is dependent on the variable.
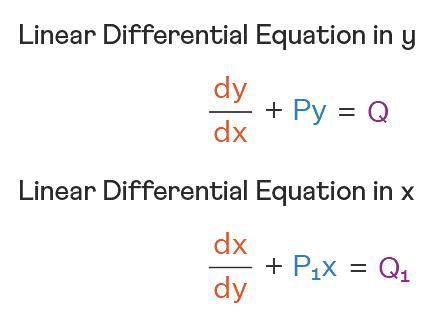
Homogeneous Differential Equations:
When the degree of f(x,y) and g(x,y) is the same, it is known to be a homogeneous differential equation.
\(\frac{dy}{dx} = \frac{a_1x + b_1y + c_1}{a_2x + b_2y + c_2}\)
Read More: Differential Equations