Question:
The coordinates of the point P which is equidistant from the three vertices of the △AOB as shown in the figure is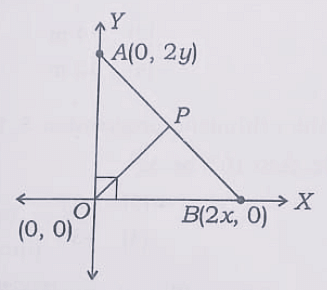
The coordinates of the point P which is equidistant from the three vertices of the △AOB as shown in the figure is
Updated On: May 7, 2024
- \((x,y)\)
- \((y,x)\)
- \((\frac x2,\frac y2)\)
- \((\frac y2,\frac x2)\)
Hide Solution
Verified By Collegedunia
The Correct Option is A
Solution and Explanation
The correct option is (A): \((x,y)\).
Was this answer helpful?
0
0
Top Questions on Distance Formula
- What is the distance between point P(1, 2, 4) and Q(4,-2, 1) in a 3-D plane?
- CUET (PG) - 2023
- Mathematics
- Distance Formula
- If point \(B(0, 1)\) is equidistant from points\( A(5, -3) \)and \(C(x, 6)\), then find the values of \( x\)
- CUET (UG) - 2023
- Mathematics
- Distance Formula
- The distance between the points (2, 3) and (4, 1) is
- TS POLYCET - 2022
- Mathematics
- Distance Formula
- The mid-point of the line segment joining the points (2, 7) and (12, -7) is
- TS POLYCET - 2022
- Mathematics
- Distance Formula
- The distance of the point A(a, b, c) from the x-axis is
- BCECE - 2017
- Mathematics
- Distance Formula
Questions Asked in AP POLYCET exam
- If the volume of a cylinder is 500 m3 and the area of its base is 25 m2, then its height (in m) is
- AP POLYCET - 2024
- Volume of Cube, Cuboid and Cylinder
- Find the 10th term of the arithmetic progression \(5,1,-3,-7,..….\)
- AP POLYCET - 2024
- Arithmetic Progressions
- If a sin 45°= b cosec 30°, then the value of \(\frac {a^4}{b^4}\) is
- AP POLYCET - 2024
- Trigonometry
- The ratio of the sum and product of the roots of the quadratic equation \(7x^2-12x+18=0\) is
- AP POLYCET - 2024
- Quadratic Equations
- The speed of light in vacuum is c. The speed of light in a medium of refractive index \(\frac 43\) is
- AP POLYCET - 2024
- Light - Reflection and Refraction
View More Questions