Question:

The compressibility factor for a real gas at high pressure is :

Updated On: Apr 30, 2024
  • 1+RT/Pb1 + RT/Pb
  • 11
  • 1+Pb/RT1 + Pb /RT
  • 1−Pb/RT1 - Pb/RT
Hide Solution
collegedunia
Verified By Collegedunia

The Correct Option is C

Solution and Explanation

(P+aV2)(V−b)=RT\left(P+\frac{a}{V^{2}}\right)\left(V-b\right) = RT at high pressure aV2\frac{a}{V^{2}} can be neglected PV−Pb=RTPV - Pb = RT PV=RT+PbPV = RT + Pb PVRT=1+PbRT\frac{PV}{\text{RT} } = 1 + \frac{Pb}{RT} Z=1+PbRT;Z>1Z = 1+\frac{Pb}{RT}\quad;\quad Z > 1 at high pressure
Was this answer helpful?
1
0

Top Questions on Van Der Waals equation

View More Questions

Questions Asked in AIEEE exam

View More Questions

Concepts Used:

Van Der Waals Equation

Van der Waals equation is an equation relating the relationship between the pressure, volume, temperature, and amount of real gases.

Read More: Derivation of Van Der Waals Equation

Derivation of Van der Waals equation:

For a real gas containing ‘n’ moles, the equation is written as

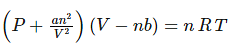
Where, P, V, T, n are the pressure, volume, temperature and moles of the gas. ‘a’ and ‘b’ constants specific to each gas.

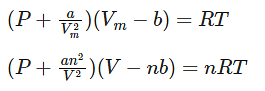
Where,

Vm: molar volume of the gas

R: universal gas constant

T: temperature

P: pressure

V: volume

Thus, Van der Waals equation can be reduced to ideal gas law as PVm = RT.

The equation can further be written as;

  1. Cube power of volume:
  2. Reduced equation (Law of corresponding states) in terms of critical constants:

Units of Van der Waals equation Constants

a: atm lit² mol-²

b: litre mol-¹