The amount of Beta rays in 10 minutes of the sun's rays is how many times the amount of IR rays in 3 minutes of the sun's rays?

The amount of Beta rays in 10 minutes of the sun's rays is how many times the amount of IR rays in 3 minutes of the sun's rays?

Show Hint
- 1.44
- 1.33
- 1.66
- 1.55
The Correct Option is C
Solution and Explanation
Step 1: Per-minute quantities from the pie chart.
Beta rays share \(= 5\%\) \(\Rightarrow\) Beta/min \(= \dfrac{5}{100}\times 3600 = 180\) units/min.
IR rays share \(= 10\%\) \(\Rightarrow\) IR/min \(= \dfrac{10}{100}\times 3600 = 360\) units/min.
Step 2: Compute required amounts for the given times.
Beta in \(10\) minutes \(= 180 \times 10 = 1800\) units.
IR in \(3\) minutes \(= 360 \times 3 = 1080\) units.
Step 3: Form the ratio (times as many).
\(\dfrac{\text{Beta in 10 min}}{\text{IR in 3 min}} = \dfrac{1800}{1080}\).
Reduce: divide numerator and denominator by \(60\) \(\Rightarrow \dfrac{30}{18} = \dfrac{5}{3} = 1.\overline{6}\).
So ratio \(= 1.666\ldots \approx \boxed{1.66}\).
Top Questions on Pie Charts
- The following pie-chart shows the amount collected by a shopkeeper by selling four different food items in degrees. The total amount collected is Rs.64,800. The amount collected by selling Chinese dishes is approximately what percentage more than the amount collected by selling Bengali dishes?

- The following pie-chart shows the amount collected by a shopkeeper by selling four different food items in degrees. The total amount collected is Rs.64,800. Find the average amount collected from the sales of Bengali dishes, Punjabi dishes and Gujarati dishes.

- Company D produced 75% more iron in 2014 than produced by it in 2013. What percent of iron produced in 2014 was produced by company D?

- The production of iron by company A in 2013 is what percent of the total iron produced by all the companies during the given year?

- Study the pie chart and table and answer the questions
Store Respective ratio of number of linen kurtis to cotton kurtis sold A 7:5 B 5:6 C 3:2 D 5:3 E 4:3 F 7:3 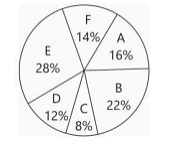
Number of kurtis (linen and cotton) sold by store D is what percent more than the number of linen kurtis sold by store B?
Questions Asked in SNAP exam
- The sum of first n terms of an A.P. is $S_n = n^2 + 4n$. Find the 10th term.
- SNAP - 2025
- Arithmetic and Geometric Progressions
- A shopkeeper marks up the price by 25% and then gives a discount of 20%. If Cost price is Rs. 800, find the Selling Price.
- SNAP - 2025
- Profit and Loss
- Find a number that leaves remainder 3 when divided by 7, and 2 when divided by 5.
- SNAP - 2025
- Number Systems
- A certain sum of money, invested at certain rate of Compound Interest, compounded annually, Amounts to Rs.8820 in 2 yrs and Rs. 9261 in 3 yrs. Find the Principal.
- SNAP - 2025
- SI & CI
- If Tan\(\theta\) + Cot\(\theta\) = 4, find Tan\(^2\theta\) + Cot\(^2\theta\).
- SNAP - 2025
- Trigonometry