The solubility of MX2–type electrolytes is 0.5 × 10–4 Mole/lit. then find out the Ksp of electrolytes :
The solubility of MX2–type electrolytes is 0.5 × 10–4 Mole/lit. then find out the Ksp of electrolytes :
5 × 10–12
25 × 10–10
1 × 10–13
5 × 10–13
The Correct Option is D
Solution and Explanation
The correct option is (D) : 5 × 10–13
An electrolyte MX2 undergoes dissociation as follows :
MX2\(\rightleftharpoons\)M+2+2X− Concentration MX2 M+2 X− Initial concentration 1 0 0 Concentration at Equilibrium 1-s s 2s Thus from the above condition we can say that, Ksp=s×(2s)2=4×(s)3 Here, s (the solubility ) is 0.5×10−4mole/lit. ∴ Ksp =4×(0.5×10−4)3 ∴ Ksp=5×10−13
Top Questions on Equilibrium
- Which of the following statements is/are true about equilibrium?
- KCET - 2025
- Chemistry
- Equilibrium
Consider the following equilibrium, $$ \text{CO(g)} + \text{H}_2\text{(g)} \rightleftharpoons \text{CH}_3\text{OH(g)} $$ 0.1 mol of CO along with a catalyst is present in a 2 dm$^3$ flask maintained at 500 K. Hydrogen is introduced into the flask until the pressure is 5 bar and 0.04 mol of CH$_3$OH is formed. The $ K_p $ is ...... x $ 10^7 $ (nearest integer).
Given: $ R = 0.08 \, \text{dm}^3 \, \text{bar} \, \text{K}^{-1} \, \text{mol}^{-1} $
Assume only methanol is formed as the product and the system follows ideal gas behavior.- JEE Main - 2025
- Chemistry
- Equilibrium
The pH of a 0.01 M weak acid $\mathrm{HX}\left(\mathrm{K}_{\mathrm{a}}=4 \times 10^{-10}\right)$ is found to be 5 . Now the acid solution is diluted with excess of water so that the pH of the solution changes to 6 . The new concentration of the diluted weak acid is given as $\mathrm{x} \times 10^{-4} \mathrm{M}$. The value of x is _______ (nearest integer).
- JEE Main - 2025
- Chemistry
- Equilibrium
A body of mass $m$ is suspended by two strings making angles $\theta_{1}$ and $\theta_{2}$ with the horizontal ceiling with tensions $\mathrm{T}_{1}$ and $\mathrm{T}_{2}$ simultaneously. $\mathrm{T}_{1}$ and $\mathrm{T}_{2}$ are related by $\mathrm{T}_{1}=\sqrt{3} \mathrm{~T}_{2}$. the angles $\theta_{1}$ and $\theta_{2}$ are
- JEE Main - 2025
- Physics
- Equilibrium
- According to Le Chatelier's principle, in the reaction \( \text{CO}(g) + 3\text{H}_2(g) \rightleftharpoons \text{CH}_4(g) + \text{H}_2\text{O}(g) \), the formation of methane is favoured by
- KCET - 2025
- Chemistry
- Equilibrium
Questions Asked in NEET exam
- Consider the diameter of a spherical object being measured with the help of a Vernier Callipers. Suppose its 10 Vernier Scale Divisions (V.S.D.) are equal to its 9 Main Scale Divisions (M.S.D.). The least count in the M.S. is 0.1 cm and the zero of V.S. is at -0.1 cm when the jaws of Vernier callipers are closed. If the main scale reading for the diameter is \(M = 5\) cm and the number of coinciding vernier division is 8, the measured diameter after zero error correction, is:
- NEET (UG) - 2025
- Measurement of length
- De-Broglie wavelength of an electron orbiting in the \(n = 2\) state of hydrogen atom is close to (Given Bohr radius = 0.052 nm):
- NEET (UG) - 2025
- de broglie hypothesis
- Which chromosome in the human genome has the highest number of genes?
- NEET (UG) - 2025
- Human genome
- In a certain camera, a combination of four similar thin convex lenses are arranged axially in contact. Then the power of the combination and the total magnification in comparison to one lens will be, respectively:
- NEET (UG) - 2025
- Images Formed By Lenses
AB is a part of an electrical circuit (see figure). The potential difference \(V_A - V_B\), at the instant when current \(i = 2\) A and is increasing at a rate of 1 amp/second is:
- NEET (UG) - 2025
- Electromagnetic Induction and Inductance
Concepts Used:
Law of Chemical Equilibrium
Law of Chemical Equilibrium states that at a constant temperature, the rate of a chemical reaction is directly proportional to the product of the molar concentrations of the reactants each raised to a power equal to the corresponding stoichiometric coefficients as represented by the balanced chemical equation.
Let us consider a general reversible reaction;
A+B ↔ C+D
After some time, there is a reduction in reactants A and B and an accumulation of the products C and D. As a result, the rate of the forward reaction decreases and that of backward reaction increases.
Eventually, the two reactions occur at the same rate and a state of equilibrium is attained.
By applying the Law of Mass Action;
The rate of forward reaction;
Rf = Kf [A]a [B]b
The rate of backward reaction;
Rb = Kb [C]c [D]d
Where,
[A], [B], [C] and [D] are the concentrations of A, B, C and D at equilibrium respectively.
a, b, c, and d are the stoichiometric coefficients of A, B, C and D respectively.
Kf and Kb are the rate constants of forward and backward reactions.
However, at equilibrium,
Rate of forward reaction = Rate of backward reaction.
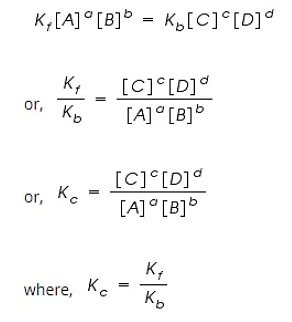
Kc is called the equilibrium constant expressed in terms of molar concentrations.
The above equation is known as the equation of Law of Chemical Equilibrium.