Question:
In the given figure the value of angle ‘x’ is _________
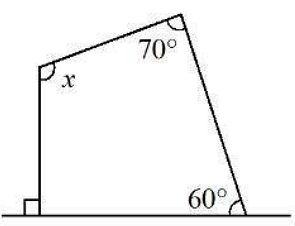
In the given figure the value of angle ‘x’ is _________
Updated On: Sep 12, 2024
- 130°
- 120°
- 140°
- 110°
Hide Solution
Verified By Collegedunia
The Correct Option is C
Solution and Explanation
The correct option is (C):140°.
Was this answer helpful?
0
0
Top Questions on Geometry
- ABCD is a rectangle where points C and D have coordinates (−2, 0) and (2, 0), respectively. If the area of the rectangle is 24, what is the best way to describe the equation of the line AB?
- If the area of a rectangle is 60 sq. cm and its length is 4 cm more than its breadth, what is its perimeter?
- A farmer has a triangular plot of land. One side of the plot, henceforth called the base, is 300 feet long and the other two sides are equal. The perpendicular distance, from the corner of the plot, where the two equal sides meet, to the base, is 200 feet.
To counter the adverse effect of climate change, the farmer wants to dig a circular pond. He plans that half of the circular area will be inside the triangular plot and the other half will be outside, which he will purchase at the market rate from his neighbour. The diameter of the circular plot is entirely contained in the base and the circumference of the pond touches the two equal sides of the triangle from inside.
If the market rate per square feet of land is Rs. 1400, how much does the farmer must pay to buy the land from his neighbour for the pond? (Choose the closest option.) - Consider a right-angled triangle ABC, right angled at B. Two circles, each of radius r, are drawn inside the triangle in such a way that one of them touches AB and BC, while the other one touches AC and BC. The two circles also touch each other (see the image below).
If AB = 18 cm and BC = 24 cm, then find the value of r.
- Given below are two statements
Statement I =If two chords XY and ZT of a circle intersects internally at point P,then PX-PYPZ-PT
Statement II =If two chords XY and ZT of a circle intersect internally at point P,then PXZ and PTY are similar triangles
In the light of the above statements, choose the correct answer from the options given below
View More Questions
Questions Asked in CUET exam
- Who devised the concept of Intelligence Quotient (IQ)?
- CUET (UG) - 2024
- Psychological attributes
- Two resistances of 100 \(\Omega\) and 200 \(\Omega\) are connected in series across a 20 V battery as shown in the figure below. The reading in a 200 \(\Omega\) voltmeter connected across the 200 \(\Omega\) esistance is _______.
Fill in the blank with the correct answer from the options given below- CUET (UG) - 2024
- Current electricity
- Two parallel plate capacitors of capacitances 2 \(\mu F\) and 3 \(\mu F\) are joined in series and the combination is connected to a battery of V volts. The values of potential across the two capacitors \(V_1\) and \(V_2\) and energy stored in the two capacitors \(U_1\)and \(U_2\) respectively are related as_____
Fill in the blank with the correct answer from the options given below- CUET (UG) - 2024
- Electrostatics
- As per data collected in 2011, arrange the following Indian states in terms of child sex-ratio from lowest to highest:
(A) Punjab
(B) Haryana
(C) Tamil Nadu
(D) Sikkim
Choose the correct answer from the options given below:- CUET (UG) - 2024
- Social Inequality and Exclusion
- A molecule X associates in a given solvent as per the following equation:
X ⇌ (X)n
For a given concentration of X, the van’t Hoff factor was found to be 0.80 and the
fraction of associated molecules was 0.3. The correct value of ‘n’ is:- CUET (UG) - 2024
- Solutions
View More Questions