Question

If V_A and VV_B are the potentials of the two points A and B, what will be the correct relation between the electric field and the potential difference between the points? The distance between the points is d.

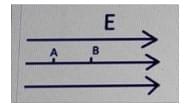
• A. V_A-V_B = Ed
• B. V_A- V_B = \(\frac{d}{E}\)
• C. V_B- V_A = Ed
• D. V_A-V_A = \(\frac{E}{d}\)

Answer 1

The Correct Option is A

We need to determine the correct relationship between the electric field \( E \) and the potential difference between two points \( A \) and \( B \), with potentials \( V_A \) and \( V_B \), separated by distance \( d \), as shown in the diagram where the electric field \( E \) points from \( A \) to \( B \). The options are: A) \( V_A - V_B = \frac{d}{E} \), B) \( V_A - V_B = Ed \), C) \( V_B - V_A = Ed \), D) \( V_A - V_A = \frac{E}{d} \).

1. Understanding Electric Potential and Field:
The electric field \( E \) is related to the electric potential \( V \) by the equation:

\( E = -\frac{\Delta V}{\Delta x} \)
where \( \Delta V \) is the potential difference over a distance \( \Delta x \), and the negative sign indicates that the field points in the direction of decreasing potential.

2. Analyzing the Diagram:
The electric field \( E \) points from point \( A \) to point \( B \), meaning \( A \) is at a higher potential than \( B \) (since the field points from higher to lower potential). Thus, \( V_A > V_B \), and the potential difference is:

\( V_A - V_B > 0 \)
The distance between \( A \) and \( B \) is given as \( d \).

3. Relating Potential Difference to Electric Field:
For a uniform electric field (assumed here, as the field lines are parallel), the potential difference between two points is:

\( V_{\text{initial}} - V_{\text{final}} = E \cdot d \)
Since the field points from \( A \) to \( B \), \( A \) is the initial point (higher potential) and \( B \) is the final point (lower potential):

\( V_A - V_B = E \cdot d \)

4. Evaluating the Options:
- Option A: \( V_A - V_B = \frac{d}{E} \). This is dimensionally incorrect (units of \( \frac{\text{m}}{\text{V/m}} = \text{m}^2/\text{V} \), not potential) and does not match the formula.
- Option B: \( V_A - V_B = Ed \). This matches our derived expression and has correct units (\( \text{V/m} \cdot \text{m} = \text{V} \)).
- Option C: \( V_B - V_A = Ed \). Since \( V_A > V_B \), \( V_B - V_A \) is negative, but \( Ed \) is positive, so this is incorrect.
- Option D: \( V_A - V_A = \frac{E}{d} \). The left-hand side is zero, and the right-hand side is nonzero with incorrect units (\( \text{V/m} / \text{m} = \text{V/m}^2 \)), so this is incorrect.

Final Answer:
The correct relationship between the electric field and the potential difference is: \( V_A - V_B = Ed \) So, the correct option is A.