Question:
Given the following Bayesian Network consisting of four Bernoulli random variables and the associated conditional probability tables :
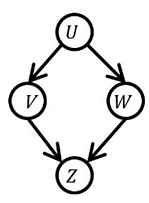
P(.) U = 0 0.5 U = 1 0.5
P(V = 0| .) P(V = 1| .) U = 0 0.5 0.5 U = 1 0.5 0.5 P(W = 0| .) P(W = 1| .) U = 0 1 0 U = 1 0 1
P(Z = 0| .) P(Z = 1| .) V = 0 W = 0 0.5 0.5 V = 0 W = 1 1 0 V = 1 W = 0 1 0 V = 1 W = 1 0.5 0.5
The value of P(U = 1, V = 1, W = 1,Z= 1) = ______. (rounded off to three decimal places)
Given the following Bayesian Network consisting of four Bernoulli random variables and the associated conditional probability tables :
The value of P(U = 1, V = 1, W = 1,Z= 1) = ______. (rounded off to three decimal places)
| P(.) | |
| U = 0 | 0.5 |
| U = 1 | 0.5 |
| P(V = 0| .) | P(V = 1| .) | |
| U = 0 | 0.5 | 0.5 |
| U = 1 | 0.5 | 0.5 |
| P(W = 0| .) | P(W = 1| .) | |
| U = 0 | 1 | 0 |
| U = 1 | 0 | 1 |
| P(Z = 0| .) | P(Z = 1| .) | ||
| V = 0 | W = 0 | 0.5 | 0.5 |
| V = 0 | W = 1 | 1 | 0 |
| V = 1 | W = 0 | 1 | 0 |
| V = 1 | W = 1 | 0.5 | 0.5 |
Updated On: Jul 9, 2024
Hide Solution
Verified By Collegedunia
Correct Answer: 0.125
Solution and Explanation
The correct answer is 0.125
Was this answer helpful?
0
0
Top Questions on Random variables
If the probability function for a random variable \( x \) is given as \( f(x) = \frac{x+3}{15} \) when \( x = 1, 2, 3 \), find the sum of the values of the probability distribution for \( x \).
- CUET (PG) - 2025
- Economics
- Random variables
- Suppose that the random variable \( X \) takes on the values: -1, 0, and 2 with probabilities \( \frac{1}{8} \), \( \frac{1}{2} \), and \( \frac{3}{8} \) respectively. Find the expected value of \( X \).
- CUET (PG) - 2025
- Economics
- Random variables
- If \(f(X) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}; -\infty<x<\infty\) and \(Y = |X|\), then E(Y) is
- CUET (PG) - 2025
- Statistics
- Random variables
- Moment generating function of a random variable Y, is \( \frac{1}{3}e^t(e^t - \frac{2}{3}) \), then E(Y) is given by
- CUET (PG) - 2025
- Statistics
- Random variables
- If, \(f(X) = \frac{C\theta^x}{x}\); \(x = 1,2, \dots\); \(0<\theta<1\), then E(X) is equal to
- CUET (PG) - 2025
- Statistics
- Random variables
View More Questions
Questions Asked in GATE AR exam
- The ceiling function of a real number \( x \), denoted by \( ce(x) \), is defined as the smallest integer that is greater than or equal to \( x \). Similarly, the floor function, denoted by \( fl(x) \), is defined as the largest integer that is smaller than or equal to \( x \). Which one of the following statements is NOT correct for all possible values of \( x \)?
- Two cars, P and Q, start from a point X in India at 10 AM. Car P travels North with a speed of 25 km/h and car Q travels East with a speed of 30 km/h. Car P travels continuously but car Q stops for some time after traveling for one hour. If both cars are at the same distance from X at 11:30 AM, for how long (in minutes) did car Q stop?
- GATE AR - 2025
- GATE ME - 2025
- GATE PE - 2025
- Direction sense
- A final year student appears for placement interview in two companies, S and T. Based on her interview performance, she estimates the probability of receiving job offers from companies S and T to be 0.8 and 0.6, respectively. Let \( p \) be the probability that she receives job offers from both the companies. Select the most appropriate option.
- GATE AR - 2025
- Probability
P and Q play chess frequently against each other. Of these matches, P has won 80% of the matches, drawn 15% of the matches, and lost 5% of the matches.
If they play 3 more matches, what is the probability of P winning exactly 2 of these 3 matches?In a regular semi-circular arch of 2 m clear span, the thickness of the arch is 30 cm and the breadth of the wall is 40 cm. The total quantity of brickwork in the arch is _______ m\(^3\). (rounded off to two decimal places)
- GATE AR - 2025
- Architecture
View More Questions