A series LCR circuit connected to a variable frequency 230 V source. L = 5.0 H, C = 80mF, R = 40 Ω.
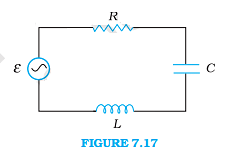
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
(c) Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency
A series LCR circuit connected to a variable frequency 230 V source. L = 5.0 H, C = 80mF, R = 40 Ω.

(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
(c) Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency
Solution and Explanation
Inductance of the inductor, L = 5.0 H Capacitance of the capacitor, C = 80 µH = 80 × 10−6 F Resistance of the resistor, R = 40 Ω Potential of the variable voltage source, V = 230 V (a) Resonance angular frequency is given as:
\(ωr=\frac{1}{√LC}=\frac{1}{√5X80X10^{-6}}=\frac{10^3}{20}=50 rad/s\)
Hence, the circuit will come in resonance for a source frequency of 50 rad/s. (b) Impedance of the circuit is given by the relation:
\(Z=\sqrt(R^2+(X_L-X_C)^2)\)At resonance, \(X_L=X_C,Z=R=40 Ω\)
Amplitude of the current at the resonating frequency is given as:\(I°=\frac{V°}{Z}\)
Where, V°=Peak voltage = \(√2V=I°=\frac{√2V}{Z}=\frac{√2×230}{40}=8.13 A\)
Hence, at resonance, the impedance of the circuit is 40 Ω and the amplitude of the current is 8.13 A. (c) rms potential drop across the inductor,
(VL)rms=IxωrL Where,
\(Irms=\frac{I°}{√2}=\frac{√2V}{√2Z}=\frac{230}{40}=\frac{23}{4}A=(VL)rms=\frac{23}{4}x50x5=1437.5V\)
Potential drop across the capacitor:
\((V_c)rms=I=\frac{1}{w_rc}=\frac{23}{4}X\frac{23}{4}X\frac{1}{50X80X10^{-6}}=1437.5V=230V\)
Potential drop across the resistor:
\((VR)rms=IR=\frac{23}{4}X40=230V\)
Potential drop across the LC combination:
\(VLC=I(X_L-X_C)\)
At resonance, \(X_L=X_C,V_LC=0\)
Hence, it is proved that the potential drop across the LC combination is zero at resonating frequency.
Top Questions on Alternating Current Circuits
- A lamp “50 watt and 100 volt” is to be connected to AC mains of 200 volt 50 Hz. Calculate the capacity of condenser required in series of lamp.
- UP Board XII - 2025
- Physics
- Alternating Current Circuits
- A voltage \( v = v_0 \sin \omega t \) applied to a circuit drives a current \( i = i_0 \sin (\omega t + \phi) \) in the circuit. The average power consumed in the circuit over a cycle is:
- CBSE CLASS XII - 2025
- Physics
- Alternating Current Circuits
- Differentiate between the peak value and root mean square value of an alternating current. Derive the expression for the root mean square value of alternating current, in terms of its peak value.
- CBSE CLASS XII - 2025
- Physics
- Alternating Current Circuits
- The resistance of 8 ohm and inductive reactance of 6 ohm are connected in series in an alternating current circuit. The impedance of circuit will be :
- UP Board XII - 2025
- Physics
- Alternating Current Circuits
- An AC power supply of 220 V at 50 Hz, a resistor of 20\( \Omega \), a capacitor of reactance 25\( \Omega \) and an inductor of reactance 45\( \Omega \) are connected in series. The corresponding current in the circuit and the phase angle between the current and the voltage is, respectively :
- NEET (UG) - 2025
- Physics
- Alternating Current Circuits
Questions Asked in CBSE CLASS XII exam
- If \[ f(x) = \begin{cases} \frac{\log(1 + ax) + \log(1 - bx)}{x}, & \text{for } x \neq 0 \\ k, & \text{for } x = 0 \end{cases} \] is continuous at $x = 0$, then the value of $k$ is:
- CBSE CLASS XII - 2025
- Continuity and differentiability
- Verify that lines given by \( \vec{r} = (1 - \lambda) \hat{i + (\lambda - 2) \hat{j} + (3 - 2\lambda) \hat{k} \) and \( \vec{r} = (\mu + 1) \hat{i} + (2\mu - 1) \hat{j} - (2\mu + 1) \hat{k} \) are skew lines. Hence, find shortest distance between the lines.}
- Calculate the value of the current passing through the battery in the given circuit diagram.

- CBSE CLASS XII - 2025
- Current electricity
- Sara and Tara were partners in a firm. Their capitals as on 1st April, 2023 were ₹ 6,00,000 and ₹ 4,00,000 respectively. On 1st October, 2023, Tara withdrew ₹ 1,00,000 for personal use. According to the partnership deed, interest on capital was allowed @ 8% p.a.
The amount of interest allowed on Tara’s capital for the year ended 31st March, 2024 was :- CBSE CLASS XII - 2025
- Partnership Accounts
- Assertion (A): If $| \mathbf{a} \times \mathbf{b} |^2 + | \mathbf{a} \cdot \mathbf{b} |^2 = 256$ and $| \mathbf{b} | = 8$, then $| \mathbf{a} | = 2$.
Reason (R): $\sin^2 \theta + \cos^2 \theta = 1$ and $| \mathbf{a} \times \mathbf{b} | = | \mathbf{a} | | \mathbf{b} | \sin \theta$ and $ \mathbf{a} \cdot \mathbf{b} = | \mathbf{a} | | \mathbf{b} | \cos \theta$.- CBSE CLASS XII - 2025
- Vector Algebra
Concepts Used:
LCR Circuit
An LCR circuit, also known as a resonant circuit, or an RLC circuit, is an electrical circuit consist of an inductor (L), capacitor (C) and resistor (R) connected in series or parallel.

Series LCR circuit
When a constant voltage source is connected across a resistor a current is induced in it. This current has a unique direction and flows from the negative to positive terminal. Magnitude of current remains constant.
Alternating current is the current if the direction of current through this resistor changes periodically. An AC generator or AC dynamo can be used as AC voltage source.
